Suite Fibonacci : la géométrie sacrée dans la nature

Leonardo Fibonacci, encore appelé Léonard de Pise, est un mathématicien italien né en 1175 à Pise, et mort en 1250. Il est célèbre grâce à la suite de nombre qui porte son nom : la suite de Fibonacci.

En réalité, cette suite était déjà connue des indiens, mais Léonardo étant marchand, il en compris l'importance et la mit en lumière.

La suite de Fibonacci en détail:

Dans son ouvrage Liber Abaci (1202) il met en évidence la suite en exposant la croissance d'une population de lapins. Grâce à sa formule, il peut calculer la population de lapins de la saison suivante à partir des quantités des saisons précédentes.

1- La population des lapins:

Il part des hypothèses suivantes:

1. Un couple de lapin est placé dans un enclos fermé,
2. Le couple génère un autre couple en seul mois,
3. Ils enfantent dans le second mois après leur naissance
4. Chaque début de mois, une paire susceptible de procréer engendre exactement une nouvelle paire,
5. Les lapins ne meurent jamais.

Question : combien de couples naissent de cette paire en une année ?

janvier : 1 couple
février : 1 couple
mars : 1+1= 2 couples
avril : 1+2 = 3 couples
mai : 2+3 = 5 couples
juin : 3+5 = 8 couples
juillet : 5+8 = 13 couples
aout : 8+13 = 21 couples
septembre : 13+21 = 34 couples
octobre : 21+34 = 55 couples
novembre : 34+55 = 89 couples
décembre : 55+89 = 144 couples

2- Nombre de Fibonacci : la formule:

Fn+2 = Fn+1 + Fn

avec Fn le nombre de couples de lapins au début du mois n

Jusqu'à la fin du deuxième mois, la population se limite à 1 couple , soit F1 = F2 = 1

Au troisième mois, le couple de lapins a deux mois et engendre un autre couple, d'où F3 = 2

3- Quelques applications:

A- Dans le triangle de Pascal: la somme des diagonales forme la suite de Fibonacci (nombres en rouge sur le schéma).

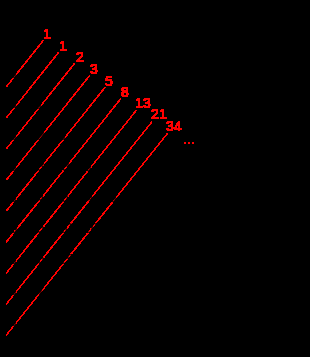
B - La spirale d'or:
En géométrie, c'est une spirale logarithmique avec un facteur de croissance au nombre d'or.

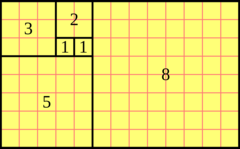
Ce schéma (source Wikipedia) est particulièrement utile pour comprendre comment se construit une spirale aux divines proportions. Il faut partir des deux nombres 1; 1+1 = 2, soit le coté du carré 2, puis 1+2 = 3, soit le coté du carré 3, puis 2+3 = 5, le coté du carré 5 et enfin 3+5 = 8, c'est à dire le coté du carré 8.

Et à partir de ce schéma, on peut construire la spirale au nombre d'or ci-dessous:

C - Dans la nature :

Cette spirale d'or est très connue car on la retrouve dans la nature au travers des coquilles des escargots et des nautiles; en effet leur coquille grandit selon cette divine proportion, c'est à dire le nombre d'or.

On la retrouve également dans les fleurs; en effet certaines fleurs ont toujours un nombre de pétales de la suite de Fibonacci. C'est le cas des marguerites, des boutons d'or, des lys...

Cette suite peut également être observée sur les pommes de pins, les choux fleurs ou encore les ananas, en forme de spirales.

Le nombre d'or:

Ce nombre mystérieux, connu depuis la nuit des temps, serait l'expression ultime de l'harmonie et de la perfection.
Symbolisé par la lettre Phi, sa formule mathématique est    

Sa valeur approchée est : 1,618 033 988...

Encore appelé divine proportion ou section dorée, il est défini en géométrie comme l'unique rapport a/b  entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c'est-à-dire lorsque :

Cette proportion s'applique à plusieurs figures géométriques comme, le rectangle, le triangle, la spirale, le pentagramme...

La géométrie sacrée et le nombre d'or:

Bien d'autres formes géométriques ont un lien direct avec le nombre d'or ou la divine proportion.

Il s'agit par exemple de la fleur de vie, des solides de Platon, du cube de Métatron, de la Vesica Piscis, du Sri Yantra ou même du fameux symbole Yin Yang.

Le fameux dessin de Léonard de Vinci, l'Homme de Vitruve", est lui-même tracé selon le nombre d'or. Il représente un homme aux proportions parfaites.

La fleur de vie est une onde de forme qui harmonise et équilibre tout ce qui l'entoure; elle permettrait ainsi d'élever le taux vibratoire des personnes et des lieux. En fait cette figure de géométrie sacrée joue le rôle de point central, car on peut en déduire beaucoup d'autres figures, comme la graine de vie, le germe de vie, l'arbre de vie, le merkaba et bien plus encore. Et toutes ces figurent ont une symbolique sacrée et sont en relation avec le nombre d'or.

En conclusion:

Il est clair que la géométrie sacrée, telle qu'elle est présente dans la nature, ne nous a pas encore livré tous ses secrets. Peut être pourrait-elle servir de portail inter dimensionnel à l'homme, dans sa quête de savoir et d'exploration.