Une accélération identique à une pression acoustique

Bonjour,

Le 05 janvier 2010, un internaute a publié ce message sur le forum de physique de Futura-sciences, pour demander des explications:

Sa demande a à peine été entendue, mais l'on y trouve quand même une réponse très intéressante d'un ancien modérateur de ce forum (LPFR):

Les conséquences d'une telle observation (l'échantillon de Léonpolou a été effectué plusieurs fois) laissent le chercheur "sidéré", si l'on tient compte strictement des observations relatées. Une chose est certaine: si les valeurs en accélération (c.a.d. des m¹/sec²) sont identiques aux valeurs en pression (m²/sec²), cela signifie clairement que ce qu'il y a une dimension d'espace au numérateur qui n'est pas fonctionnelle..

Mais qu'est-ce que cela peut bien vouloir dire ?  Il y a deux possibilités de réponses conjointes, qui ne s'excluent pas mutuellement:

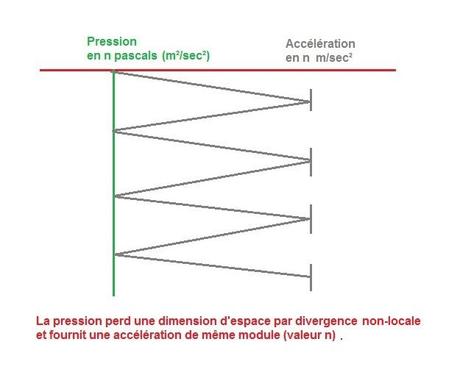
1.  Cela veut dire que l'espace n'existe pas, parce qu'il est "acquis" en tant que partie intégrante du domaine de définition sonore: l'espace de l'onde sonore n'est pas traversé par les sons comme on s'y attendrait, mais il cet espace lui-même est créé par les sons. Sa valeur "cursive" ne vaut que 1 et sa valeur exponentielle vaut 0 : m⁰ = 1.  Donc les dimensions métriques des pressions en m²/sec² valent les dimensions en m¹/sec² à condition qu'elles perdent une dimension d'espace par divergence non-locale.

Donc tout l'espace de l'Univers vaut 1, parce que sa dimension est en m⁰ . Seuls les sons sont capables de créer un pont pour rejoindre tout point de l'espace, de l'Univers.

Il y a plusieurs façons de montrer les différences dimensionnelles?. Mais nous sommes bientôt capables de montrer leur non-localité (à suivre) spatiale.

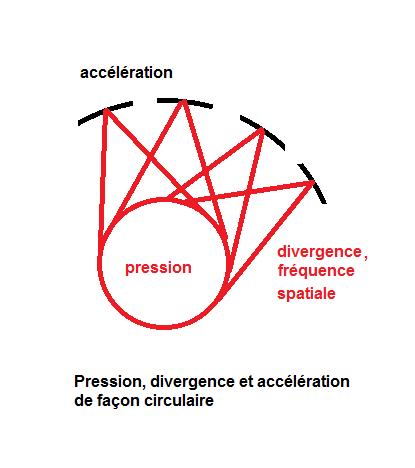
Ci-contre: le cercle extérieur de l'accélération reste déplié,  mais se regroupe autour du cercle intérieur, contrairement au dessin précédent.

Au lieu d'avoir deux droites représentants la pression et l'accélération, nous avons deux courbes à l'extrémité de surfaces circulaires.

Mais il est possible de montrer -encore mieux-, de façon volumique, que l'on ne peut dire en fait quel est le cercle des pressions ou celui des accélérations, puisque ces deux "ronds" sont des représentations.

Projecteur non-local invisible, créateur par divergence

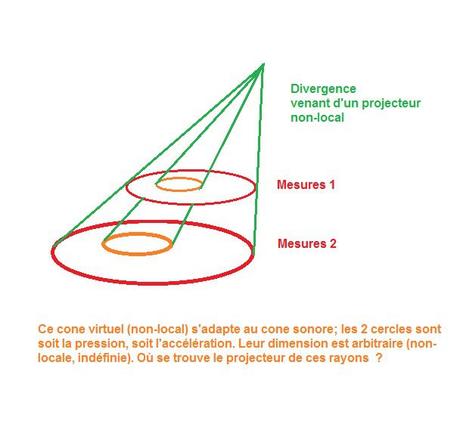
De façon volumique, l'on peut mettre en valeur la divergence elle-même. C'est évidemment une forme de perspective et dans ce cas, comme toute perspective, elle est arbitraire.. mais pas fausse, si l'on conserve l'ordre successif des mesures.

L'on s'aperçoit évidemment que la source, l'origine des rayons, montrant cette "qualité" ne se situe nulle part dans cette dimension. 

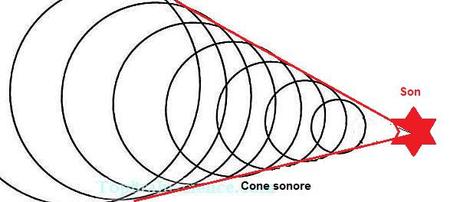
Sauf qu'au niveau spatial, elle "colle" parfaitement au cone sonore, que l'on voit ci-dessous.

2. Cela veut dire que le temps des pressions est différent de celui des accélérations : ci-dessus, pour retrouver les mêmes valeurs de pression que les accélérations, nous avons modifié stratégiquement une des données du numérateur (dans les m²). A présent, nous allons modifier une des données du dénominateur, dans les sec²..

Mais les maths y sont diférentes: les secondes carrées doivent être modifiées "ensemble". Prenons un exemple par l'absurde: est-ce que 3/9 est égal à 3/12 ? Non, sauf si l'on parvient à réduire le nombre 12, en le comprimant jusques 9  !

Cette chose-là est possible avec les sec² .. Si le temps se réduit, c.a.d. si le temps cinématique s'accélère aux différents endroits de l'espace (sur le parcours du cône sonore) au fur et à mesure qu'on s'éloigne de la source du bruit, alors les valeurs de pression et d'accélération seront égales.

3. Distorsions entre pressions et intensités sonores

La réponse de LPFR peut nécessiter la naissance d'un modèle correspondant à l'existence d'un cône sonore (et certainement plusieurs, disposés autour de la manifestation d'un son) qui "s'avance à travers l'espace" à la manière d'un porte-voix; admettons que ce cône soit d'une envergure d'angle de 60° ..

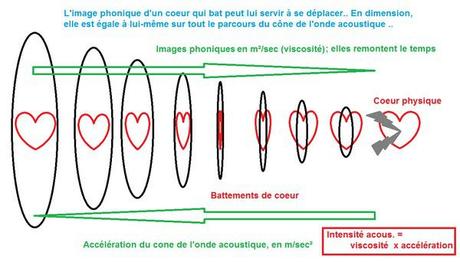
Ce cône présente tout au long de son "trajet" depuis la source du son une surface ronde d'égale pression frontale.  Or le calcul de la surface de pression, à travers l'espace, varie très différemment de celui de l'intensité sonore.

Int sonore = Viscosité cinématique x accélération.

A suivre, article en construction