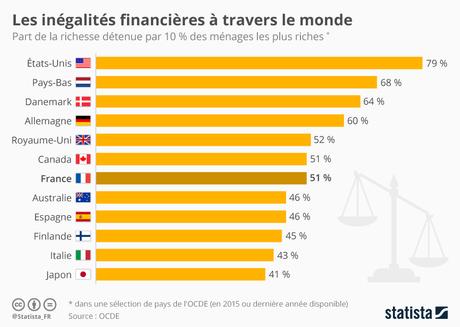
Les inégalités sociales sont inévitables
Nous savons tous que dans notre société, les richesses sont inégalement réparties, même si nous ignorons généralement à quel point c'est vrai. Mais nous nous trompons sur la cause de cette répartition inégale des richesses. Nous croyons qu'elle est due à des choix politiques qui privilégient presque toujours les riches par rapport aux pauvres, et sur le fait bien connu que les banques "ne prêtent qu'aux riches". Nous nous trompons ! Une récente étude publiée dans Scientific Américan et Pour la Science le démontre : les inégalités sociales sont inévitables. Le système économique dans son ensemble est instable et conduit inéluctablement a un monde où dans lequel une petite poignée de milliardaires posséderont la quasi totalité des richesses, sauf s'il y a une politique fiscale très agressive vis à vis des riches. Ceci est la conséquence d'un théorème mathématique.

Si les gens savaient comment les
richesses sont réparties...
...Ils descendraient tous manifester dans la rue. Mais ils ne savent pas ! Dans un papier de 2011, deux scientifiques ont analysés les croyances à propos des inégalités. Ils sont demandé à plus de 5000 américains de deviner le pourcentage de richesse (économies, propriétés, placements, etc.) possédé par chaque cinquième de la population :
Imaginez une pizza représentant toute la richesse du pays. Quel pourcentage de la pizza appartient aux 20% des gens les plus riches ? Et quelle est la part de pizza que possèdent les 40% de gens les moins riches ?
Le résultat est que les gens pensent en moyenne que les 20% de gens les plus riches posséderaient 50% de la pizza, et que les 40% les plus pauvres en posséderaient 9%.
La réalité est totalement différente ! Les 20% les plus riches possèdent en réalité 84% de la richesse, et les 40% de gens plus moins riches n'en ont que... 0,3%. Les inégalités réelles sont bien plus grandes que nous le pensons. Nous n'avons aucune idée de à quel point les riches sont très riches (voir la page comment vivent les milliardaires sur ce site).
Mais il y a pire...
La richesse se concentre de plus en plus, c'est un fait. Et cela s'accentue ! en 2010, 388 milliardaires possédaient autant que la moitié la plus pauvre de la population mondiale. En 2020, on estime ce nombre à 26. Ce mouvement de concentration de la richesse semble inéluctable.
Mais pourquoi ?
Eh bien, la réponse, surprenante, de Bruce M Boghosian, professeur de mathématiques à l'université Tufts (USA) et auteur de l'article de Scientific American, est que les inégalités de richesses résultent d'une simple bizarrerie... mathématique. Pour la comprendre, procédons par étapes.
Première étape, souvenons-nous que ajouter un pourcentage à la valeur d'un bien, c'est en réalité multiplier la valeur de ce bien par une valeur déterminée. Par exemple lorsque je rajoute 10% à un article, en réalité je multiplie sa valeur par 1,1. Lorsque je retire 10% à un article, en réalité je multiplie sa valeur par 0,9. Et lorsque je retire 10%, puis que plus tard j'ajoute 10% (ou le contraire) au même article, en réalité j'ai multiplié la valeur de l'article par 1,1 x 0,9 = 0.99 ; Au final, mon article a perdu 1% de sa valeur.
Maintenant, imaginons que vous soyez dans un casino et que l'on vous propose de jouer à un jeu : Vous devez placer 100 € sur la table de jeu, et le croupier tire à pile ou face (avec une pièce non truquée). Si pile sort, le casino ajoute 20% à la valeur qui se trouve sur la table (donc cela fera 120 €). Si au contraire c'est face qui sort, le croupier retire 17% de la valeur qui se trouve sur la table (donc il restera 83€). Toutes les trente secondes, le croupier tire à pile ou face et ajoute 20% ou retranche 17% en fonction du résultat du tirage. Vous pouvez jouer aussi longtemps que vous le désirez, et vous pouvez retirer votre argent à tout moment. Devez-vous jouer à ce jeu ?
Deux raisonnements : sont possibles :
Raisonnement un : J'ai une chance sur deux de gagner 20%, et une chance sur deux de perdre 17%. En partant de 100€ :Mon espérance de gain est donc, de (1/2 x 20€) - (1/2 x 17€) = 1,50 €. Elle est donc positive et donc j'ai intérêt à jouer.
Raisonnement deux : Hmm. en moyenne, au bout d'un grand nombre de tirages pile sortira presque aussi souvent que face. Chaque fois que pile sort, ma mise est multipliée par 1,2. Chaque fois que face sort, elle est multipliée par 0,83. Au bout d'une série, disons de 5 pile et de 5 face (dans n'importe quel ordre), ma mise sera multipliée par (1,2 x 0,83)5 = 0,9965 = 0,9802 et donc de mes 100 €, il ne me restera plus que 98 euros et 2 centimes. Je n'ai pas intérêt à jouer.
Et c'est ce second raisonnement qui est le bon !
Quel rapport avec la répartition des richesses ?
Imaginons un modèle de l'économie d'un pays dans lequel un grand nombre d'acteurs économiques (des particuliers, des entreprises) échangent en permanence des biens et des services. Plus précisément, à chaque transaction, un acteur échange un bien ou un service contre de l'argent avec un autre acteur, et bien entendu chacun cherche à tirer le bénéfice maximal de la transaction.
Rien ne semble plus naturel qu'un échange commercial entre deux personnes se mettant d'accord sur un prix et se serrant la main. Le libre marché nous semble si naturel que nous pensons que ce système ne peut être que stable, parce que stabilité résulterait de l'équilibre entre l'offre et la demande. En fait, beaucoup de personnes pensent (c'est la base de la pensée libérale) que le libre marché, sans entraves et sans intervention de l'état ni taxes, représente le modèle économique idéal et souhaitable.
Et bien.. C'est faux ! Et nous allons le démontrer. Loin de "ruisseller" des riches vers les pauvres, la richesse en réalité tend mathématiquement à se concentrer dans les mains des plus riches.
Dans notre modèle économique, au fil du temps, les différents acteurs vont donc se livrer à des milliers d'échanges commerciaux deux à deux. A chaque fois, lorsque deux acteurs échangent, achètent ou vendent un bien ou un service, si la valeur payée est exactement égale à celle du bien échangée, la richesse des deux acteurs demeurent inchangée.
Mais naturellement,il arrive souvent que la valeur payée ne soit pas tout à fait égale à la valeur réelle du bien ou du service. Dans ce cas la richesse de l'un des acteurs augmente légèrement, et celle de l'autre diminue d'autant. En moyenne, toutefois, on se fera "berner" à peu près aussi souvent que l'on sera gagnant, et donc le système devrait être stable.
Eh bien, non ! Ceci à cause d'un fait de nature psychologique : Si je suis très riche (disons que je possède un million d'euros), et que j'achète une voiture dont la valeur réelle est de 10 000 euros, je me fiche de la payer en fait 9000 ou 11000 : ce que je gagnerai ou perdrai dans l'échange (1000 €) ne représente qu'une infime partie de ma richesse. En revanche, si je ne possède que 12 000 euros, cette voiture représente une somme très importante pour moi, donc je vais être plus dur à la négociation, et je n'accepterai pas de perdre plus de 120 € dans la transaction (disons, 1% de ce que je possède).
Donc, dans notre modèle, nous allons supposer que lors d'une transaction, la valeur qui peut être potentiellement perdue n’excédera pas une petite fraction de la richesse du plus pauvre des deux partenaires qui participent à l'échange.
Et alors ?
Résumons-nous : nous allons simuler un modèle économique dans laquelle chaque acteur posséderait au départ la même somme, disons 10 000 €. Nous allons simuler des milliers de transactions. Cerains acteurs vont donc devenir plus riches ou plus pauvres que d'autres (au moins temporairement). Dans chaque transaction, on tire à pile ou face. Si pile sort, le plus pauvre deux deux acteurs impliqué est gagnant. Si face sort, le plus riche est gagnant. La somme gagnée ou perdue sera un petit pourcentage de la la richesse de l'acteur le plus pauvre avant la transaction. Plus précisément, si pile sort, le pauvre gagne 20% de ce qu'il avait avant. Si face sort, il perd 17% de ce qu'il possédait. Ça ne vous rappelle rien ?
Bien sûr ! Notre jeu de casino décrit plus haut... Attend, attend, que va-t-il se passer ?
Ce qui va se passer, c'est la même chose que pour notre jeu de casino : la ruine progressive des acteurs les plus pauvres. Le système économique est instable ; les inégalités, même minimes, vont s'accentuer, et s’accentuer encore, et au final on aboutira à une oligarchie, c'est à dire une situation dans laquel une personne (ou entreprise) possédera la quasi totalité du patrimoine mondial et les autres ne se contenteront que de miette misérables.
C'est d'autant plus surprenant que la situation de départ était une égalité totale, et que les transactions sont parfaitement symétriques : puisque le vainqueur est tiré à pile ou face, chaque acteur gagne et perd en moyenne le même nombre de fois. Il y a même à chaque fois un avantage pour le pauvre parce soit il gagne 20% soit il perd 17%, avec la même probabilité.
Oh la, minute ! D'où sortent ces chiffres de 20% et 17% ? Qui nous dit qu'avec d'autres chiffres, le système ne sera pas stable ? Vous avez parfaitement raison de poser ces questions ! C'est pourquoi j'ai fabriqué pour vous un simulateur avec lequel vous allez pouvoir jouer !
Jouez avec notre simulateur économique !
Dans ce simulateur, on imagine une population de 10 000 acteurs économiques qui se livrent à des échanges de biens et de services entre eux. Au départ chaque acteur possède 10 000 €. Il y a donc cent millions d'euros au total en circulation dans notre petit pays virtuel.
A chaque étape, le simulateur choisira deux acteurs économique au hasard et simulera une transaction entre les deux. Lors de chaque transaction le bien échangé peut être légèrement surévalué ou sous-évalué, et il y aura donc un gagnant et un perdant, mais chacun a exactement une chance sur d'eux d'être gagnant (ou perdant) dans la transaction.
Si c'est le plus pauvre des des deux acteurs qui y gagne, il va gagner au maximum un certain pourcentage p de sa propre richesse. SI c'est le riche qui gagne, il va gagner au maximum un certain pourcentage q de la richesse du plus pauvre. C'est vous qui allez choisir ces pourcentages p et q
Ensuite, on va faire tourner le modèle jusqu'à ce qu'il ait simulé un certain nombre d'échanges, disons un million. Que va-t-il se passer ? Cliquez sur le bouton "lancer la simulation" pour le savoir !
Simulateur de la répartition des richesses économiques
Nombre d'échanges simulésPourcentage p de gain max du plus pauvre (1 à 100) : par rapport à sa fortune
Pourcentage q de perte max du plus pauvre (1 à 100) : par rapport à sa fortune
Vous constatez que quelle que soient les données d'entrée, la richesse tend (plus ou moins doucement) à se concentrer dans les mains d'une poignée de personnes. Plus le nombre d'échanges simulés augmente, plus l'Indice de Gini augmente. L'indice de Gini augmente donc inexorablement vers 1 avec le temps.
Mais l'indice de Gini, qu'est-ce que c'est ?
Tout simplement une mesure de l'inégalité de richesse (ou de revenus). 0 correspond à une égalité parfaite (toutes les personnes ont les mêmes richesses), et 1 à une inégalité totale (où une personne posséderait tout). On voit sur la carte ci-dessous que certains pays sont plus égaux que d'autres...
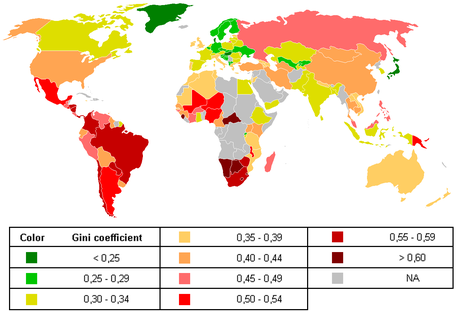
Mais que faire contre les inégalités?
La solution est évidemment d'implémenter une forme de redistribution des richesses.

Bien sûr, en pratique, la politique fiscale est une jungle. Mais simplifions là drastiquement et imaginons un impôt qui prélèverait un pourcentage identique sur chaque transaction ; cette somme serait ensuite répartie équitablement entre tout le monde.
Cette solution peut-elle annuler la "malédiction de l'inégalité inévitable ? Et oui, quel devrait être le taux de cette taxe ? Eh bien... Il n'y a qu'à la simuler !
Ce simulateur est identique au précédent à ceci près qu'à chaque transaction un pourcentage de la somme gagnée ou perdue est prélevé et redistribué équitablement à tous (même les plus riches !).
Simulateur de la répartition des richesses économiques avec impôt
Nombre d'échanges simulésPourcentage p de gain max du plus pauvre (1 à 100) : par rapport à sa fortune
Pourcentage q de perte max du plus pauvre (1 à 100) : par rapport à sa fortune
Taux d'imposition sur les transactions :
Et voila, vous constaterez que même un petit taux d'imposition (5%) suffit à faire revenir l'indice de gini dans le vert... Y a plus qu'à ?
Tous mes livres : Cliquez sur le titre qui vous intéresse






NOUVEAU ! Vous aimez ce site ? Aidez-moi !
Partagez / votez pour cette page :

