Archimède vu par Bernoulli, ou l'équation des milieux stables

Bonjour,

Statique des objets en milieu fluide

Le principe d'Archimède régit la "suspension" des objets en milieu gazeux, et la suspension et la flottaison des objets en milieu liquide, en termes de force.

Or une force F = Pression x surface

Prenons déjà l'exemple d'un bateau sur la mer.
Si l'on interprète correctement le principe d'Archimède l'on constate qu'un bateau flottant sur une mer calme a équilbré les "forces" avec elle. Mais en fait, cet équilibre est plutôt celui des pressions, depuis toute la profondeur sous l'eau jusqu'au niveau "zéro" de la mer, indépendamment des diverses étendues de surface de la coque des vaisseaux

Et à partir du moment où l'on parle de pressions, l'on peut éventuellement vérifier le principe d'Archimède comme un très intéressant cas particulier de la loi de Bernoulli: c'est l'équation des milieux stables 

Dynamique des objets en milieu fluide

A bien regarder, le premier endroit où le principe d'Archimède peut s'adapter à la loi de Bernoulli, est celui du niveau zéro de sa ligne de flottaison d'un bateau, là où la pression de l'eau est égale à zéro, ainsi que sa vitesse et, c'est plus difficile à comprendre, là où sa "hauteur" vaut zéro également !

Car n'oublions pas: pour la mer, tout ce qui flotte n'a pas de + de "hauteur" que son propre niveau, meême si, apparemment, des structures flottantes "émergent" et "immergent" certains de leurs composants. Donc la formule est la suivante :

Equation des milieux stables

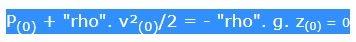
pour P = pression, rho = masse volumique du liquide, v = vitesse, g = acc. grav, et z = hauteur.
Le signe - interprète la poussée sous-marine, afin de m'en servir pour calculer plus aisément le problème du surenfoncement des bateaux quand la vitesse d'un bateau fait bouger aussi celle de l'eau de mer contre elle (v supérieur à zéro)..

A suivre, article en construction