Comme nous l’avons, la présence du carré magique se justifie abondamment :
- talisman contre la mélancolie (1.2 Astronomie, Astrologie),
- jeu formel redondant la signature (1.2 Astronomie, Astrologie),
- solution de la quadrature de la sphère (3 La question de la Sphère),
- schéma de principe de la construction du polyèdre (4 La question du Polyèdre),
Tout cela n’épuise pourtant pas la question. Dans une oeuvre à énigmes comme « Melencolia I », l’oeil désorienté, sautant d’un objet à l’autre en quête d’un sens qui se dérobe, n’en finit pas de revenir se poser sur ce tableau de nombres, dont la cohérence implacable résiste au désordre ambiant.
D’où l’idée – qui a notre connaissance n’a jamais été exploitée – que ce quadrillage numérique pourrait constituer une sorte de légende, une grille de déchiffrement de l’ensemble.
Une grille de lecture
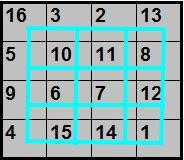
Les cases dans le carré magique peuvent être lues quatre par quatre : en colonne, en ligne, en diagonale, ou bien selon n’importe laquelle des combinaisons dont la somme est 34 (voir2 La question du Carré).
. Mais on peut tout aussi bien les regrouper par couples, puisque les cases sont symétriques par rapport au centre. Enfin elles peuvent être parcourues séquentiellement, de 1 à 16.
Si le carré magique est effectivement une grille de lecture, il faudra que les éléments de la gravure puissent également être lus quatre par quatre, ou par couples, ou dans l’ordre de la numérotation, et que toutes ces lectures aient un sens.
Est-il vraisemblable que Dürer ait pu avoir l’idée et l’ambition démesurée de construire un « carré symbolique », dans lequel les objets entretiendraient, entre eux, les mêmes relations que les nombres dans un carré magique ?
Une lecture à plat
On imagine l’intensité des contraintes, se superposant à toutes celles que nous avons déjà découvertes (les trois alignements), plus la nécessité de respecter la perspective. Sur ce dernier point cependant, remarquons que la situation est favorable : tandis que la gravure jumelle, le Saint Jérôme, est un chef d’oeuvre de perspective, celle-ci ne joue, dans Melencolia I, qu’un rôle très secondaire : condition facilitant une lecture « à plat ».
Un quadrillage sous contraintes
Il suffit de jeter un coup d’oeil sur la gravure pour vérifier qu’aucun quadrillage ne saute aux yeux : les objets sont de tailles inégales, de très petits à très grands. Certains sont posés par terre, d’autres accrochés au mur.
Plaçons-nous néanmoins dans la situation de l’archéologue et tirons nos cordeaux pour délimiter le terrain. Est-il possible de répartir en seize cases l’ensemble des objets de la gravure ?
Visiblement, les cases seront de tailles inégales : la présence massive de Melencolia repousse les objets vers les marges.
Y en aura-il assez pour remplir les seize cases ? Bien qu’il soient très inégalement répartis dans la gravure, la trentaine d’objets devrait suffire à peupler toutes les cases : certaines en possèderont même plusieurs. Il est seulement à prévoir que les plus gros objets (l’échelle, le cristal, la règle) ne rentreront pas dans une seule case.
Un point de départ
Il est logique de commencer notre quadrillage par la partie de la gravure où la densité des objets est la plus faible : le coin en haut à droite. Là, nous n’avons guère le choix : la cloche, le sablier et la balance sont des objets solitaires, qui occupent donc respectivement les cases 13, 2 et 3. Verticalement, aucune latitude non plus : le carré et les clés sont les seuls objets pouvant occuper les cases 8 et 12.
Ces quelques associations suffisent à montrer que le nombre à rechercher n’a rien à voir avec la forme de l’objet : le carré a 16 cases, mais correspond à la case 8. Le trousseau a 6 clés, mais correspond à la case 12.
De même, il serait vain de rechercher une allusion au nombre dans un détail de l’objet : il est vrai que la décoration en forme d’omega de la balance ressemble à un chiffre trois. Mais rien dans la forme de la cloche n’évoque le chiffre 13.
Une proposition de découpage
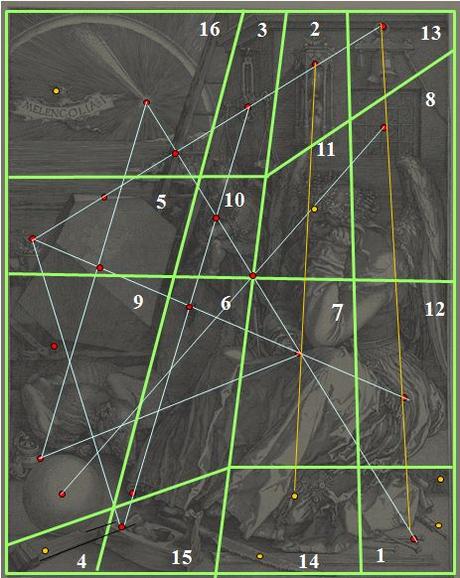
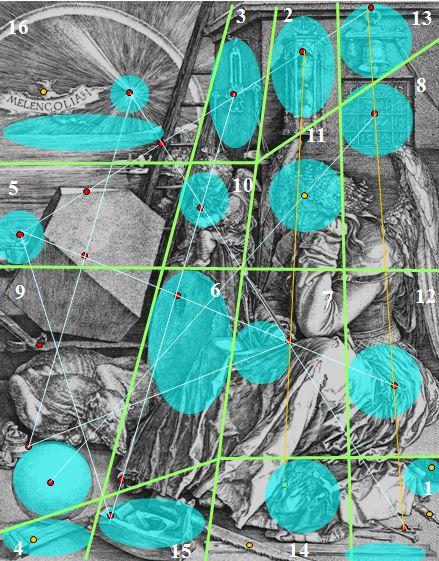
Il serait fastidieux de poursuivre case par case. Nous avons donc fait figurer, sur un même schéma, les alignements que nous avons déjà découverts, avec leurs points représentatifs (en rouge) ; et une proposition de découpage en seize cases (en vert), sur laquelle nous nous baserons pour la suite des explications.
Que ces cases aient des tracés quelque peu artificiels, empiétant parfois sur une portion d’objet, n’est pas rédhibitoire : il était impossible d’être à la fois rigoureux pour les alignements de points significatifs (qui conduisent aux différents diagrammes de la croix et de la machine) et rigoureux sur la délimitation des frontières. Peut être Dürer avait-il plutôt en tête un découpage sinueux, à la manière d’un puzzle, qu’un tracé sauvagement colonisateur, à base de segments de droites.
Si arbitraire qu’il puisse paraître à ce stade, notre découpage a néanmoins pour mérite de faire apparaître de nouveaux alignements, plus modestes que ceux que nous avons interprétés jusqu’ici (lignes orange) : ainsi les points significatifs de la cloche, du carré, du trousseau de clés et des clous sont sur une ligne verticale. De même, une ligne verticale relie les bourses et le compas au sablier, en passant par un objet qui était passé inaperçu jusqu’ici, et qui prend une importance accrue, puisqu’il est le seul à pouvoir occuper la case 11 : la couronne de Melencolia.
Pour éviter de nous reporter en permanence à la gravure, voici donc le tableau qui résume notre découpage hypothétique, et sur lequel nous allons désormais raisonner :
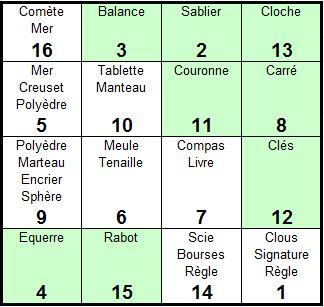
Ce quadrillage contient pratiquement tous les objets de la gravure (sauf l’échelle, l’arc en ciel et l’objet mystérieux), certains empiètant sur deux cases (la mer, le polyèdre, la règle). S’il constitue un « carré symbolique », alors il doit pouvoir être lu selon les mêmes règles de symétrie que le carré magique : par lignes, par colonnes ou par couples d’objets symétriques par rapport au centre.
L’exercice que Dürer nous propose est une sorte de « tarot dirigé » : au lieu de tirer des images au hasard, nous avons pour contrainte de les extraire du tableau dans un certain ordre, quatre par quatre ou deux par deux, et de deviner le sens qui s’en dégage.
Les huit cases qui ne contiennent qu’un seul objet (en grisé) seront les plus difficiles : par exemple, la cloche, dans la case 13, devra avoir un sens en tant qu’élément de la première ligne, mais aussi en tant qu’élément de la dernière colonne.
Les autres cases contiennent plusieurs objets, ce qui laisse heureusement une marge de manoeuvre pour les interprétations : par exemple, dans la case 14, nous pourrons retenir comme symbole la scie pour la lecture par colonnes, et les bourses pour la lecture par couples.
Nous ne saurions trop engager le lecteur, avant de lire les « solutions » ci-après, à tenter lui-même l’exercice.
La lecture orthogonale
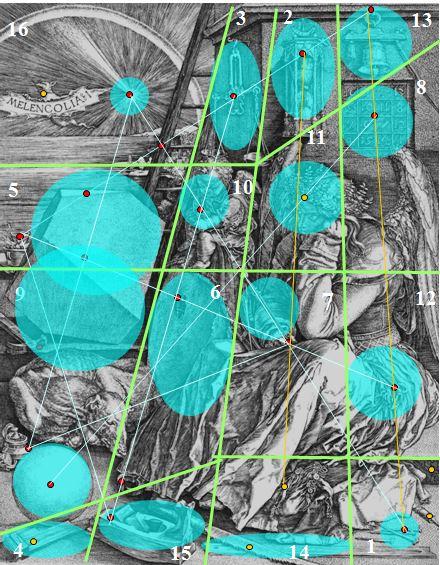
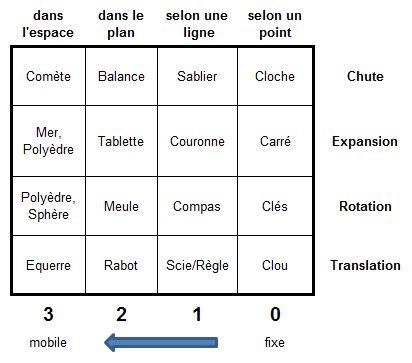
Pour cette interprétation, nous devons retenir, dans les seize cases, les objets qui permettent de donner un libellé générique aux quatre lignes et aux quatre colonnes.
La troisième ligne : la rotation
Nous suggérons de commencer par cette ligne, car nous l’avons déjà interprétée (voir 7.4 La Machine Alchimique) : les clés, le compas, la meule et le cristal sont tous situés sur l’axe de rotation de la machine alchimique, et classés selon l’ordre croissant des degrés de liberté : les clés illustrent la rotation sur un point, le compas selon une ligne, la meule dans le plan et le cristal dans l’espace. Se rajoute au cristal, dans la case 9, la sphère qui représente également les rotations dans l’espace.
La quatrième ligne : la translation
Pouvons-nous trouver des objets qui illustrent l’idée de translation, classés également selon l’ordre croissant des degrés de liberté ? Un clou qu’on enfonce matérialise la translation sur un point ; la scie et la règle illustrent la translation le long d’une ligne, le rabot la translation dans un plan. Enfin, l’équerre glisse dans le plan de la planche à dessin ; mais elle peut également, en tant que gabarit à moulure, se translater parallèlement à elle même : c’est donc une excellente image des translations dans les trois directions de l’espace.
La première ligne : la chute
Pour poursuivre la série, il nous faut un troisième type de mouvement, lui aussi ordonné par degré de liberté croissant : la chute est un bon candidat.
Le battant de la cloche est un objet immobilisé dans sa chute par un point d’accrochage. Le filet de sable s’écoule en traçant une ligne. Les deux plateaux de la balance choient, chacun à son tour, dans le plan du fléau. Enfin, la météorite s’abat où elle veut, selon une trajectoire erratique.
La deuxième ligne : l’expansion
L’interprétation de cette ligne est moins évidente : de même que la translation complète la rotation, il nous faudrait un « mouvement » qui complète, ou inverse la chute. Or les corps inanimés choient, mais ne remontent pas spontanément. Ce qui monte, ce qui croît, ce qui augmente, ce sont les êtres animés. Voyons si cette idée d’expansion, peut se lire sur la deuxième ligne.
Le carré magique illustre l’expansion autour d’un point : les nombres progressent, de 1 à 16 et remplissent toutes les cases, en s’organisant autour du point central. Les tiges végétales de la couronne croissent selon des lignes. Le dessin ou l’écriture du putto remplit le plan de la tablette. Enfin, le polyèdre et la mer sont deux exemples d’expansion dans l’espace.
La deuxième ligne illustre donc un mouvement tout aussi naturel que la chute : l’expansion, la propension des êtres à remplir la forme qui leur est impartie.
Voici les objets retenus pour cette lecture, et l’interprétation des lignes et des colonnes :
Le tableau représente une sorte de physique des mouvements possibles : la translation et la rotation pour les corps d’ici bas, la chute pour les objets d’en haut ; enfin, pour les êtres en devenir, l’expansion vers la forme qui les régit.De droite à gauche, le tableau de lit comme une progression de l’immobilité vers le mouvement maximal.
La lecture radiale
Pour cette lecture, nous devons donner une interprétation aux huit couples de cases symétriques par rapport au point central du carré.
Carré et sphère : la Matière
La case 6 ne contient que le carré magique, tandis que sa symétrique, la case 9, nous laisse l’embarras du choix.
Nous avons largement commenté ( 3 La question de la Sphère et 5.2 Analyse Elémentaire) le rapport qui unit le carré à la sphère : celle-ci représente la matière dans son état terrestre, opaque et obtuse, telle qu’elle se présente aux yeux de l’homme ; alors que le carré magique, qui réalise la quadrature du cercle, représente la matière magnifiée, décomposée selon les Eléments, telle qu’elle apparaît sous le regard de Dieu.
Cloche et équerre : la Verticale
Ces objets sont célibataires dans les cases 13 et 4 : nous ne pouvons donc que moduler les interprétations que nous leur avons déjà données lors de la lecture orthogonale. Le battant de la cloche, qui illustrait l’idée de chute immobilisée, représente également la verticale naturelle que prennent tous les corps pesants. L’équerre, qui illustrait les translations dans l’espace, peut être également vue comme représentant la verticale artificielle que l’homme peut élever à partir d’un plan. C’est donc l’idée de verticale qui unifie ces deux objets.
Mer et règle : l’Horizontale
Les cases 1 et 16 sont plus riches en objets : il est tentant de retenir, pour notre lecture radiale, deux éléments qui entretiennent le même type de relation que dans le couple précédent : la mer, paradigme de l’horizontale naturelle et la règle, instrument de l’horizontale artificielle.
Creuset, mer et clés : le Pouvoir
La case 12 ne contient que les clés, dont Dürer nous a dit qu’elles symbolisaient le pouvoir : pouvoir de l’homme puisqu’elles ouvrent des coffres ou des maisons (la ville à l’horizon comporte six maisons, autant que de clés dans le trousseau).
Nous nous attendons donc à trouver dans la case 5 des symboles du pouvoir de la nature : et effectivement, la mer et le creuset sont des images convaincantes des deux forces élémentaires que sont l’Eau et le Feu.
Balance et bourses : la Richesse
Le second élément dont Dürer nous a donné le signification se trouve en case 14 : les bourses représentent la richesse, mais la richesse telle qu’elle apparaît aux yeux des hommes, exprimée en espèces sonnantes et trébuchantes. En face, la balance, seul objet de la case 3, fait allusion à une autre forme de richesse : la richesse morale, celle qui sera pesée par Dieu au jour du Jugement.
Sablier et rabot : la Durée
D’un point de vue physique, ces deux objets évoquent l’abrasion : érosion naturelle à l’échelle des siècles, pour le sable ; arrachage artificiel et rapide des copeaux, pour le rabot. D’un point de vue mystique , le sablier, qui accueille dans son royaume réversible une multitude d’égaux obéissants et polis, donne une image du Temps tel qu’il se présente pour Celui qui a l’Eternité devant lui. Tandis que le rabot qui aplanit la planche irréversiblement, illustre le passage du temps à l’échelle de la vie humaine.
Durée divine et durée humaine : tel pourrait donc être le dialogue du sablier et du rabot.
Tablette et livre : la Pensée
La tablette et le livre sont deux instruments de la pensée : la tablette montre la pensée en action, le livre illustre la connaissance figée, accumulée et transmise : inspiration divine, bibliothèques humaines…
Couronne et meule : le Travail
Enfin, la couronne évoque le cycle de la végétation, la pousse des plantes : le travail de Dieu au travers de la nature. La meule est l’instrument de travail de son partenaire, l’homme, le meunier, auquel il a été donné pouvoir d’exploiter et de transformer à son profit la nature.
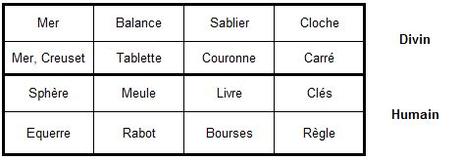
Les huit couples que nous venons de décrire participent tous de la même dialectique : celle du naturel et de l’artificiel, du divin et de l’humain. Et, très logiquement, les symboles du divin se retrouvent dans la moitié supérieure du carré, ceux de l’humain dans la moitié inférieure. La lecture radiale n’est donc finalement qu’une nouvelle méditation sur le thème de la similitude entre le haut et le bas.
Afin de bien percevoir la logique d’ensemble, remplaçons les objets par la notion qu’ils symbolisent :
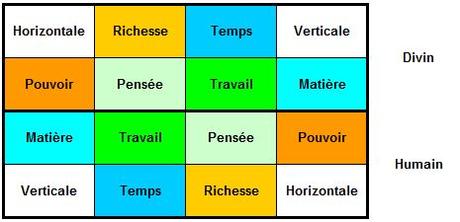
Les huit notions ne sont pas indépendantes, mais peuvent être regroupées deux par deux :
- les deux directions, Horizontale et Verticale, occupent les cases d’angle ;
- les deux symboles mentionnés par Dürer, Pouvoir et Richesse, constituent un « rectangle penché » ;
- Forme et Durée donnent le rectangle symétrique ;
- Enfin, Travail et Pensée occupent le carré central.
Ainsi la lecture radiale permet de décomposer le tableau en quatre motifs de somme 34.
Mais la magie du carré fait apparaître d’autres sujets de méditation, tout aussi pertinents : l’association « Richesse et Temps » donne également un rectangle à somme 34, ainsi que « Matière et Pouvoir ».
Les deux diagonales révèlent des thèmes quasiment maçonniques : « Pensée et Horizontale » d’une part, « Travail et Verticale » d’autre part, que nous pourrions traduire par « la pensée aplanit et le travail élève ». Mais l’inépuisable carré contient également un thème bergsonien : « Matière et Pensée » ; un thème marxiste : « Travail et Pouvoir », un thème libéral « Travail et Richesse »…
Nous ne prétendons pas que le carré symbolique ainsi reconstitué soit exactement celui que Dürer avait en tête lors de la conception de la gravure. Nous l’avons construit en effet par deux opérations éminemment subjectives : la sélection d’un objet représentatif de chaque case, puis l’abstraction de l’objet au symbole.
Mais nous prétendons que Dürer a chercher à répartir les objets dans la gravure selon des symétries identiques à celles du carré magique. Tâche complexe, oulipienne, mais pas impossible grâce aux quelques degrés de liberté que l’artiste s’est accordé : une case peut contenir plusieurs objets, un objet peut déborder sur deux cases, et quelques objets ne font pas partie du carré.
Camerarius et ses araignées
Nous avons déjà parlé de la description de la gravure par Camerarius (voir 7.3 A Noir). La dernière phrase a fait douter de ses dons d’observation ou de mémoire (excusable en 1541, s’il n’avait pas la gravure sous les yeux). En voici la traduction :
« On peut voir aussi comment ont été exprimées par l’artiste, à la fenêtre, des toiles d’araignées et celles-ci guettant leur victime, entre autres choses significatives, avec les lignes les plus fines. » [1]
Camerarius a-t-il confondu le carré magique et ses chiffres serpentiformes, avec une toile et ses araignées voraces ? Ou les « lignes les plus fines » traduisent-elles le souvenir qu’il aurait gardé des rayons de la comète, induisant une confusion entre chauve-souris et araignée ?
Mais surtout, est-il concevable que sa description, par ailleurs plutôt fidèle, se conclue par une telle approximation ?
Dürer et ses toiles
Revenir au latin s’impose :
« Cernere etiam est quasi ad fenestram a pictore aranearum telas (taela) , et venationem harum, inter alia huius naturae indicia, tenuissimis lineis expressa » [1a]
Pour rendre à Camerarius son honneur, il suffit de reprendre sur deux point la traduction donnée par Büchsel : le mot « quasi » est essentiel, et l’expression « venationem harum » ne signifie pas « la chasse à la victime » mais « la chasse à celles-ci (les toiles) ».
Voici donc la nouvelle traduction que nous proposons :
« Il nous faut aussi discerner, dans une sorte de fenêtre, les toiles d’araignées tracées par l’artiste, et les débusquer, entre différents indices de même nature, exprimées avec les lignes les plus subtiles ».
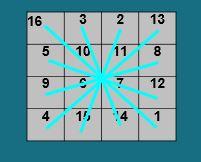
Ainsi Camerarius ne fabule pas avec des toiles d’araignée imaginaires : il veut simplement suggérer, par cette image, la méthode de lecture par lignes, inspirée par cette « sorte de fenêtre » que constitue le carré magique. Et il est vrai que la grille que nous avons tracée évoque singulièrement l’oeuvre des arachnides.
« Melencolia I » n’est pas un diagramme à déchiffrer : mais une toile d’araignée dans laquelle des symboles tous reliés entre eux nous invitent à des parcours en réseau.
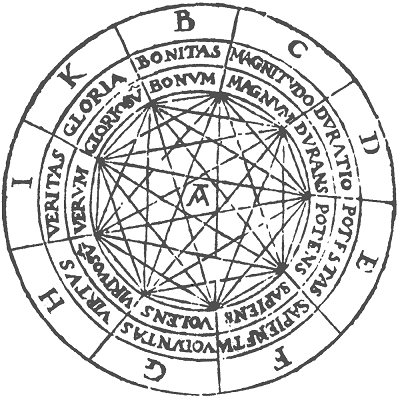L’Ars Magna, Raymond Lulle
Assez semblable, dans l’esprit, aux tableaux combinatoires de Raymond Lull, le « carré symbolique » de Dürer fonctionne comme un associateur d’idées, un support pour des méditations guidées.
Illustrations de « Von der Artzney Bayder Glück des guten und widerwertigen »,
1532,Augsbourg [2], traduction du « De Remediis Utriusque Fortuna » de Petrarque
Il y a bien sûr quelque chose d’excessif dans cette prétention à tirer des fils entre toutes choses :
« Rien ne répugne à la sagesse comme l’excès d’acuité, rien pour un philosophe n’est plus pénible qu’un sophiste ; d’après les Anciens, c’est pour cela que l’araignée est odieuse à Minerve : la subtilité de son ouvrage, la finesse de sa toile ne révèlent que leur fragilité et ne servent à rien. Que la pointe de l’esprit soit comme celle de l’épée : qu’elle pénètre, mais sans céder ». « Les remèdes aux deux fortunes », Petrarque, livre I,7, L’esprit
Mélancolie, vers 1803, Caspar David Friedrich
La toile d’araignée est à l’image des constructions complexes et tortueuses de l’esprit en proie à la Mélancolie.
La ruine de Vianden à travers une toile d’araignée, Victor Hugo, 13 aout 1871
Si fragiles soient-elles, elles ouvrent néanmoins une fenêtre sur le monde.
Jeu de briques
Snake
Pacman
Bubble