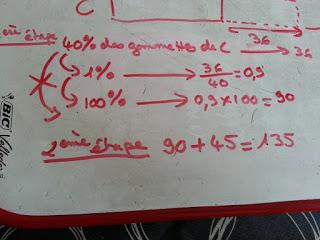Les pourcentages avec la Méthode de Singapour

Cette année de 6ème demande beaucoup de temps du lutin, investi aux devoirs. Nous avons dû faire des choix pour ne pas trop le surcharger. Le suivi de la Méthode de Singapour est passé en seconde position parce que le niveau que nous suivons dépasse un peu celui de la 6ème, soit le grade 6 aux USA (nous utilisons les propositions d'une maison d'éditions singapourienne et aussi basée aux USA, Marshall Cavendish).
Cette méthode explicite, qui a le vent en poupes depuis le rapport du mathématicien à la médaille Fields Cédric Villani, revient pendant les vacances. Parce que je ne peux décemment pas passer à côté au vu de la compréhension qu'elle apporte.Nous passons de la démarche ensemble à une pratique guidée, "à trous" avec schéma intégré, à la dernière forme: la résolution en totale autonomie. Pour les problèmes avec des pourcentages, le schéma simplifie toujours l'abstrait. Le plus compliqué reste de FAIRE le schéma, après tout est clair.
Voici le lutin en pleine démonstration: connaitre le tout quand un pourcentage est connu. Il m'avait demandé de le photographier, je n'avais pas pris la peine de noter l'énoncé mais c'est toujours intéressant de voir le schéma: une barre de 100% (représentée par la seconde flèche en partant du haut), coupée en deux parties, 60% et 40%. Les 40% représentent 480 euros, combien fait le tout (les 100%)?

Mais les problèmes se compliquent vite en appliquant des augmentations ou des diminutions par exemple. Toujours faire attention au tout qui ne correspond pas toujours au 100%.
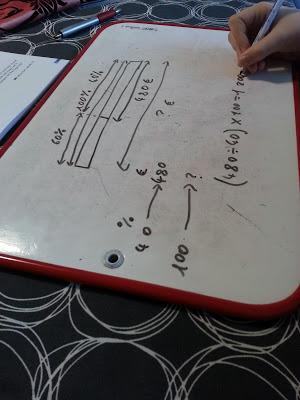
Ici une école qui augmente de 10% son effectif: après son augmentation, ils sont 1320 élèves.

Ou encore quand les parties sont en pourcentages mais aussi en fraction.
Le schéma est essentiel:- savoir combien de barre(s) mettre (2 s'il s'agit d'une comparaison ou d'un avant/ après)- savoir retrouver les parties (au nombre de combien) et le tout - savoir noter ce que nous connaissons, la somme de base (100%), les pourcentages juste au dessus de cette barre-là, les autres éléments- savoir noter ce que nous cherchons- pour un énoncé encore plus complexe, savoir distinguer le pourcentage se rapportant au total et celui se rapportant au reste (je tente de vous faire une photo plus tard).
Voici un exemple:L'énoncé (une histoire de gommettes partagées avec la question: combien y a-t-il de gommettes en tout?) et le schéma en barre associé (les 100% concernent la portion de Claude).

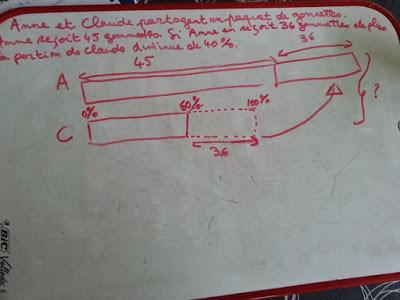
La première étape où il faut passer par la démarche unitaire ou celle du 20% (nous ne pouvons pas trouver directement un lien entre 40% et 100%)La seconde étape pour trouver le tout.