Le chenapan apprend les définitions et les propriétés par cœur pour les utiliser. Est-ce suffisant? Le processus est si normé que je me suis dit qu'un petit mode opératoire serait parfait pour ancrer tout cela.
***Bien-sûr - devrais-je dire- une visualisation peut être le préambule. C'est tellement évident avec la Méthode de Singapour que le petit d'homme suit avec moi depuis le CP: pas de manipulation concrête possible ici mais au moins une modélisation du problème. Une compréhension par le dessin est parfaite pour simplifier la question.
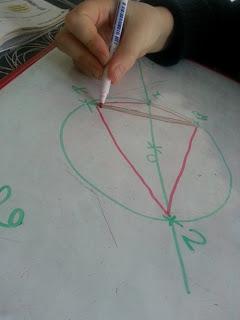
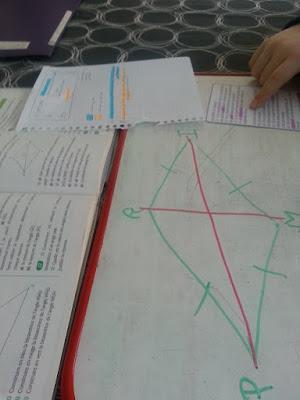
Première étape donc, reprendre le cours et dessiner à main levée la propriété en utilisant un code couleur pour bien visualiser ce que nous savons et ce que nous cherchons. Malgré le daltonisme rouge/vert du lutin, nous les avons utilisées ici.De quoi réviser les définitions (codage en vert sur la figure) et les propriétés (codage en rouge) puis de mettre en route le réflexe d'un croquis à main levée pour mieux visualiser une démonstration.
***
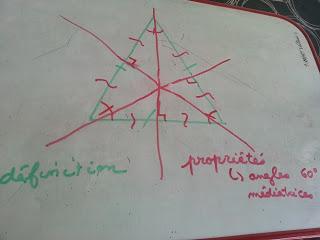
D'accord: mais la démonstration en elle-même? (dès qu'il faut démontrer, justifier, prouver mais non déduire).Il s'agit d'utiliser des formules dans le bon ordre, ici une belle présentation.Le tout est d'avoir un puzzle à remplir bien précis puis toutes les propriétés.
Il y a déjà l'idée que certains éléments sont connus et d'autres à chercher. En vert "ce que je sais" et en jaune "ce que je cherche".
Le format est:On sait que ... (données utiles prises dans l'énoncé ou le codage de la figure géométrique) 1/Or Si ... alors... (propriété ou théorème)Donc ... (conclusion: définition de la figure) 2/
1/ Ce que je sais me permet d'utiliser quel(le) théorème (propriété)?2/ De quoi ai-je besoin pour arriver à la définition de la figure?
Parce que voilà, le premier élément (les premiers trois petits points: ...) trouvé donne le second; le troisième, le dernier. Vous ne comprenez pas? Il y a correspondance, visible ici par les couleurs, encore: On sait que ***Or si *** alors ***Donc ***
Reste à connaître la propriété à utiliser. Il faudra la connaître, la retrouver par le dessin mais pour l'entrainement et les révisions, il est possible de passer par du matériel: des cartes/fiches ou tiroirs/boites de propriétés tout prêts. Par exemple là un tiroir à propriétés.
Pour la 6ème, Le bonheur en famille propose des cartes très bien faites: le recto avec la figure, le verso toutes les propriétés associées. Il manque les triangles que je vous présentais en début de billet. J'y ai fluoté les termes qui nous aident.Pour la 4ème, en partant de ce que nous cherchons, le Collège Condorcet de Dourdan propose un livret complet.Pour la 3ème, le lien Mathmaurer là.A vous de choisir, soit pour séparer chaque propriété comme une carte individuelle par conclusion (définir un quadrilatère par exemple), soit avoir un livret complet. Il faut que les propriétés soient très visibles (encadrées, fiches individuelles, fluotées etc...)
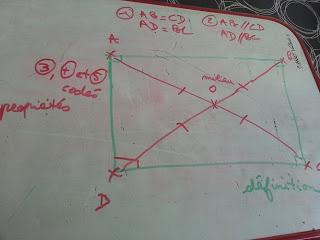
De notre côté, ce sont les cartes de 6ème et un fabuleux livret de propriétés géométriques, de la 6ème à la 3ème, mis à disposition par le Collège Louis Pergaud de Courville s/Eure. Ainsi dessiner ce que nous savons (en vert, données de l'énoncé ou la figure dessinée et codée de l'énoncé).
Mettre en évidence rouge ce que nous cherchons avec pourquoi pas la définition de la figure à démontrer.
Puis prendre le puzzle démonstration et la fiche de propriétés associées
certaines propriétés sont plus faciles à retrouver...
***
*ExogeoJ'ai vu de nombreuses propositions interactives sur le net. Bien-sûr un fabuleux logiciel Exogeo plus aussi disponible qu'avant, il serait accessible seulement si un professeur convie un élève sur le site Labomep. Des liens interactifs restent, des entrées par les hypothèses (données de l'énoncé) ou par la conclusion, ici ou là.
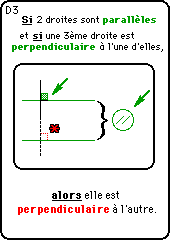*Jean-Louis Guillot
Jeu de briques
Snake
Pacman
Bubble