Le temps comme une longueur de courbe

Amaury Pouly reçoit le prix Ackermann qui récompense chaque année au niveau européen une thèse exceptionnelle dans les domaines de la logique et de la science informatique. Ses travaux, qui reposent sur la comparaison des modèles théoriques analogiques et digitaux, proposent une nouvelle vision de la complexité algorithmique, considérant le temps nécessaire à la résolution d’un problème comme la longueur de courbe d’une équation différentielle. Ces apports offrent un nouvel éclairage sur une problématique fondamentale en informatique théorique.

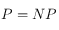
. Cette affirmation ne vous dit rien ? Elle est pourtant au cœur de l’informatique théorique, et la résolution de cette problématique aurait des conséquences très importantes dans notre vie quotidienne ! Pour bien comprendre cette question fondamentale, il faut revenir aux sources de l’informatique théorique, cette discipline qui cherche à mesurer l’efficacité des algorithmes à partir du nombre de pas de calcul (petites étapes de calcul) nécessaires pour résoudre des problèmes. En étudiant un modèle théorique des ordinateurs, symbolisé par la machine de Turing, les chercheurs ont pu ranger les problèmes en plusieurs classes. Parmi ces catégories, distingue traditionnellement les problèmes que l’on peut résoudre dans un temps appelé polynomial (la classe dite P), ce qui signifie dans un temps efficace ou du moins acceptable, et les problèmes dont on peut vérifier les solutions lorsqu’elles sont trouvées en temps polynomial (classe dite NP). Ces deux classes de complexité sont définies de manière différente et la question de savoir si ces deux classes sont effectivement distinctes est centrale pour un nombre très important d’outils numériques. C’est le cas notamment de la cryptographie. En effet, chiffrer des informations demande de s’appuyer sur des problèmes impossibles à résoudre par des attaquants. Mais comme les chercheurs ne sont pas certains que cette distinction existe réellement, potentiellement tous les problèmes pourraient être un jour résolus dans un temps polynomial grâce à un outil mathématique non encore découvert ! 

La suite sur le site du CNRS