Selection de variables predictives pour un algorithme de Machine learning du marché action

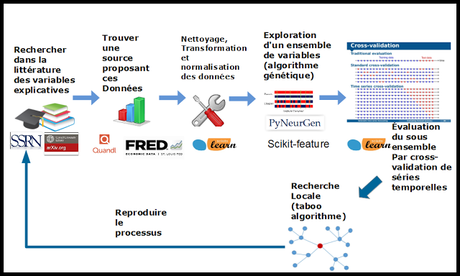
Trouver le sous-ensemble de variables explicatives qui améliore la qualité de prédiction d'un modèle: un problème difficile.

Posons d'abord le problème en termes abstraits. Supposons que nous disposons de K séries temporelles X1...Xk que nous envisageons comme potentiels prédicteurs d'une variable d’intérêt Y que nous souhaitons prédire à un horizon donné. Étant donné que nous pouvons totalement ignorer l'ordre de ces variables (les permutations ne changent pas le résultats), si nous voulions étudier toutes les combinaisons possibles de N variables (N<K) il nous faudrait évaluer 2^K combinaisons de prédicteurs, ce qui devient rapidement inexploitable pour des problèmes non triviaux.
Et il y a bien pire, les scenarios suivants peuvent se produire:
-  Deux variables supposées redondantes peuvent être prédictives lorsqu'elles sont combinées.
- Une variable inutile par elle-même peut devenir prédictive quand elle est combinée à d'autres variables
- Deux variables inutiles peuvent devenir utiles quand elles sont combinées.
- Augmenter le nombre de variable peut conduire à de l'overfitting.
Pour illustrer chacun de ces points, je vous invite à  consulter An Introduction to Variable and Feature Selection.

Utilisation des indicateurs économiques

De nombreux indicateurs économiques ont été proposés au fil des ans pour expliquer les fluctuation du marché action. La qualité de ces prédictions ont depuis été mis en causes lorsque ces variables ont été réévaluées sur des échantillons ou des intervalles différents ou pour des questions méthodologiques. Un papier célèbre de Goyal & Welsh (PDF) arguent que parmi 50 variables identifiées, aucune ne fait apparaître les propriétés décrites dans les travaux publiés originalement. Cette évaluation a été largement critiquée (par exemple Campbell & Thompson). Et le débat continue...
Ces travaux académiques ont toutefois en commun d'utiliser des outils paramétriques et/ou Bayésien basé sur des relations linéaires entre le variables (Ordinary Least Square OLS, ARD, Ridge, elasticNet), sans s'aventurer sur des algorithme d'apprentissages non paramétriques comme les arbres de décisions (Boosted Trees, Random Forest) ou les réseaux de neurones (LTSM, GRU et autres NarX). 
La littérature sur l'application de ces méthode de machine learning reste largement marginale, alors même qu'elle est d'un intérêt certain pour le praticien car les outils du machine learning comme Keras ou Scikit-Learn sont devenus maintenant d'une simplicité d’accès remarquable.
Dans cet article, je me propose d'exposer ma démarche pour sélectionner les variables explicatives dans le cadre particulier de la prédiction des marchés financiers caractérisés par un ratio bruit/signal très élevé, et par une structure qui évolue dans le temps.

Les Trois approches pour la sélection des prédicteurs dans une démarche de machine learning: Filter, Embedded & wrapper

Sans aller chercher très loin , l'article Wikipédia sur la sélection de variable (feature selection en anglais) donne une vision assez complète  du paysage moderne de la sélection de variable explicative.

L'approche Filter

Ces approches se divisent en trois catégories:L'approche filter: On  utilise ici des outils statistiques ou liés à a théorie de l'information pour isoler les variables les plus significatives parmi un ensemble, et cela indépendamment de tout algorithme d'apprentissage. Scikit-learn propose des outils dans ce sens issus de l'indicateur d'information mutuelle pour les régressions.
J'en profite pour fortement recommander à tous ceux qui sont intéressés par cette approche, de consulter avec la plus grande attention les extensions proposées par l'université Arizona State University au sein d'un package d'extension à scikit-learn appelé scikit-feature. Ce package s’intègre parfaitement au framework scikit-learn.
Dans la pratique, dans le cadre de mon application, ces méthodologies, même les plus récentes (JMI,CIFE),m'ont proposé parfois des choix de variables explicatives assez étranges... J'aimerais que le choix des variables soit basé sur un raisonnement statistique, mais dans la pratique, les variables sélectionnées sont souvent peu informatives pour les algorithmes que j'utilise (ExtraTrees, LTSM) ni même pour des ensembles de ceux-ci. Les sélections de ces algorithme donnent des résultats assez décevant dan la cross-validation de time-series (TimeSeriesSplit).

L'approche Embedded

Il s'agit ici des méthodes de sélection de variable intégrées à  la construction d'un modèle.Les modéle proposant de pondérer les variables sont nombreux : Lasso, ElasticNet, Ridge, SVM, Extra Trees, etc.
Ces modèles peuvent être utilisés directement, ou via un algorithme de Recursive Feature Elimination (RFE ou RFECV).
Ici encore, les résultats ont été decevants. Dans on cas, les méthodes de RFE ont donné des resultats trés instables à travers les classes d'actifs, les modèles choisis ou même les paramètres de Cross-Validation.  Les méthodes basés sur l'algorithme LARS n'ont pas réussi à converger. Les arbres décisionnels donnent soit beaucoup trop de variables significatives soit pas assez. Aucun modèle ne donne le même résultats qu'un autre modèle. Il est possible que ces résultats décevants soit lié à ma méconnaissance des paramètres et modalités pratiques de ces méthodes.
Mais dans tous les cas, vu le temps que j'y ai passé, ce ne sont pas vraiment des outils triviaux à utiliser.

L'approche Wrapper

Dans mon expérience, la seule méthode qui fonctionne est celle que j'appellerai la méthode ad-hoc: Dans le sens, ou elle est basée sur des sélections qui sont aléatoires initialement, et qui sont renforcées en les modifiant de manière répétée jusqu’à qu'une bonne solution soit trouvée. Cette approche nécessite d'évaluer les propositions une à une avec une cross-validation reproduisant au plus prés le scenario d'utilisation des modèles choisis. Pour ma part, je fais ma cross validation comme suit: je découpe mes données en 16 intervalles via TimeSeriesSplit. Pour éviter des résultats aberrants sur les premiers intervalles, le premier tiers de ceux-ci sont utilisés dans le training uniquement. Je choisit un modèle d’évaluation de cross-validation qui fait a moyenne entre des arbres décisionnels (Extra Trees) et un NN simple (MLPRegressor).

Parcourir l'espaces des prédicteurs avec les algorithmes génétiques et la recherche tabou.

Pour cadrer mon approche Wrapper, J'ai étudié une librairie assez marginale et peu connue qui s'appelle PyNeurGen. Cette librairie se propose de combiner les approches des algorithmes génétiques et celles des réseaux de neurones en utilisant une binarisation des formes de Backus-Naur. Cette librairie m'est utile pour deux raisons principales: elle contient une implémentation d'un réseau NarX, et surtout elle me permet de générer une population aléatoire de sous-ensemble de variables prédictives, de les évaluer, et de combiner les meilleures solutions entre elles.
Dans la pratique, comme l'univers à explorer contient 2^k combinaisons, l'algorithme peut ne jamais conserver vers une bonne solution. Par ailleurs, comme les variables peuvent se neutraliser les unes les autres, ou produire des effets non intuitifs, les solutions combinées sont rarement aussi bonnes que les deux parents qui leur ont donné leur matériel génétique.
Les avantages de cette méthode sont de proposer un ensemble initial de solution quand  le problème n'a pas été défriché.
Souvent, au lieu de rechercher une ensemble de prédicteurs à partir de rien, il est plus intéressant de partir d'une bonne solution et de rechercher des solutions adjacentes qui sont meilleures que la solution initiale. C'est le cas notamment quand on a récemment élargi notre ensemble de prédicteurs avec de nouvelles variables. Dans ce cas, on peut vouloir étudier la performance d'une substitution ou d'un ajout d'une nouvelle variable en lieu et place d'une ancienne variable, ou vérifier si l'ajout d'une nouvelle variable ne rends pas redondantes les autres variables.
Pour ces situations, j'ai implémenté un outil de recherche d'optimum local basé sur une implémentation minimale de l'algorithme de Recherche Tabou.
En partant d'un sous ensemble de variables déjà évalué (une solution), a chaque itération de cet algorithme on évalue d'autres sous ensembles où une variable a été échangée, ajoutée ou soustraite de ma solution initiale. Cette méthode donne de bon résultats.
A terme, je compte étendre cet algorithme en lui permettant d'explorer des solutions ou des combinaisons non linéaires de variables qui seront ajoutées/substituées au variables existantes (produit, division, moyennes mobiles, etc).