Superposer à une oeuvre d’art des tracés géométriques impliquant le nombre PI ou le nombre d’or, est une activité récréative qui donne des résultats colorés et étonnamment convaincants. Jusqu’à ce qu’une autre construction toute aussi mirobolante vienne concurrencer la première, puis une autre, sans autre terme que l’épuisement du stock de crayons de l’investigateur.
En règle générale, les cas où l’on peut s’accorder sur le tracé géométrique sous-tendant une composition, sont ceux où l’artiste a eu l’amabilité de nous laisser un dessin préparatoire, ou de ne pas effacer trop consciencieusement les traits de construction.
Dans le cas de la Melencolia I, fournir une nouvelle interprétation géométrique est donc aussi banal, présomptueux et promis à une rencontre rapide avec le plancher des vaches, que de tester un nouveau prototype d’aile volante depuis le troisième étage de la tour Eiffel – autre construction utopique qui, celle-là, a le mérite de tenir debout.
Nous allons donc nous limiter ici à une question géométrique particulière que pose la gravure : y-a-t-il un rapport entre le carré magique et la sphère ?
Le carré de côté quatre
Ce carré a une particularité : c’est le seul dont le périmètre P (4×4) est égal à la surface S.
Le cercle de diamètre deux
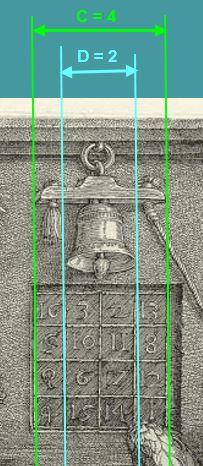
Le diamètre de la cloche mesure exactement deux cases du carré. Le cercle de diamètre D=2 a la même particularité que le carré de côté C=4 : son périmètre P (2 x Pi x 2) et égal à sa surface S (PI x 2 x 2).
La cloche et la carré magique illustrent le seul cercle et le seul carré dont le périmètre est égal à la surface.
Les problèmes de quadrature
Les problèmes de quadrature consistent à trouver un moyen géométrique pour passer du cercle au carré :
- un premier problème consiste à trouver le carré ayant le même périmètre P que le cercle initial (quadrature périmétrique) ;
- un second problème consiste à trouver le carré ayant la même surface S que le cercle initial (quadrature surfacique).
Le fait que Durer nous montre, côte à côte le seul carré et le seul cercle pour lesquels P=S est peut être destiné à attirer l’attention sur les problèmes de quadrature.
La quadrature périmétrique
Si D est le diamètre du cercle et C le côté du carré ayant le même périmètre, la relation est D = 4/PI x C.
En mesurant la sphère et le carré magique, nous trouvons justement qu’ils sont dans un rapport de 1,27 (donc très proche de 4/PI).
Le problème auquel réfléchit Melencolia, le compas à la main et la règle à ses pieds, pourrait-il être celui de la quadrature périmétrique ? Problème insoluble comme nous le savons depuis 1882 (Ferdinand von Lindemann), car le nombre PI n’est pas constructible à l’aide de ces instruments.
Le compas
Le fait que les dimensions de la sphère et du carré magique correspondent au rapport de quadrature pourrait être une simple coïncidence. Parmi les nombreux objets qui entourent Melencolia, isoler ces deux-là et prétendre qu’elle réfléchit à la quadrature du cercle n’est-il pas quelque peu réducteur ?
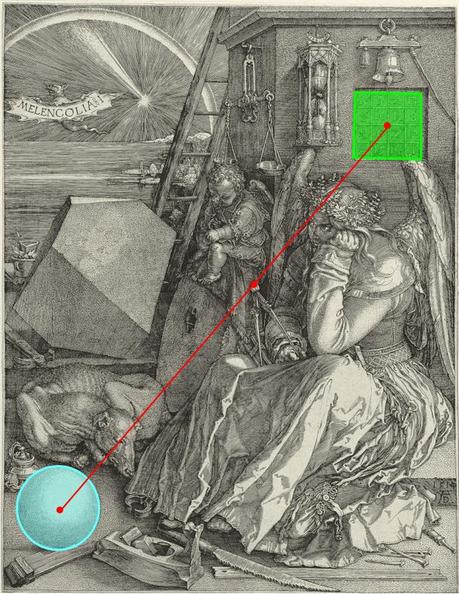
Remarquons néanmoins que la droite qui relie le centre de la sphère et le centre du carré passe… par le centre du compas.
Nombre d’or et quadrature du cercle
Par une coïncidence numérique, il se trouve que le valeur numérique du rapport de quadrature, 4/PI, est liée à autre nombre tout aussi célèbre que PI, le nombre d’or PHI :
4/PI est égal (au millième près) à Rac(PHI).
Au contraire de PI, le nombre PHI (irrationnel, mais non transcendant) peut se construire facilement avec une règle et un compas. Cette approximation miraculeuse de PI à l’aide de PHI, ouvre donc la possibilité d’une solution géométrique (presque exacte) du problème de la quadrature.
Les deux rectangles d’or
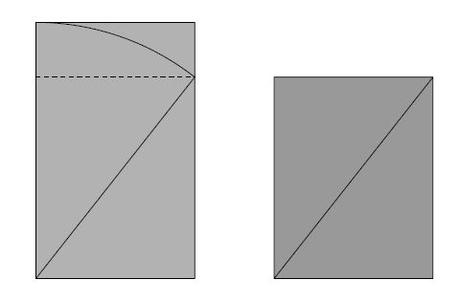Rectangles d’Or type 1 et type 2 [1]
Supposons que le petit côté d’un rectangle vaille 1. Nous pouvons construire un « rectangle d’or » de deux manières, en donnant la longueur PHI soit au grand côté (rectangle d’or type 1), soir à la diagonale du rectangle (rectangle d’or N°2). Dans ce second cas, du fait des propriétés de PHI, le grand côté a une longueur bien particulière : Rac(PHI).
Pour comparaison, à gauche et à droite les deux rectangles d’or, au centre le format A4 [1]
Dürer et le rectangle d’or
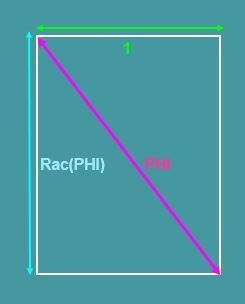
Dürer a utilisé le format du rectangle d’or type 2 pour ses trois gravures maîtresses : le « Chevalier et la Mort » en 1513, MELENCOLIA I et Saint Jérôme en 1514. Ce format très particulier n’a pas été suffisamment relevé, peut être parce que, du fait des irrégularités de l’impression et du vieillissement, le format varie légèrement selon les épreuves (à 1% près). [2]
Dans le cas de Melencolia I, le choix de ce format est particulièrement significatif :
ainsi, la gravure exhibe, dans le rapport entre sa diagonale et sa largeur, le rapport qui permet la quadrature du cercle.
Une construction inédite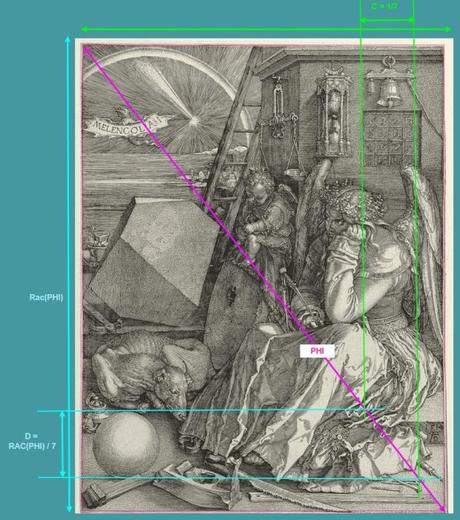
Prolongeons les deux verticales qui délimitent le carré magique, jusqu’à la diagonale descendante. Prolongeons de même les deux horizontales qui délimitent la sphère.
Ces verticales et horizontales se coupent sur la diagonale. Ceci est normal puisque la sphère et le carré et sont dans le même rapport que la hauteur de la gravure par rapport à sa largeur . Mais cette construction ne se contente pas de fournir les dimensions de la sphère et du carré : elle donne également leur position relative dans la gravure :
une fois que le carré est positionnée, la sphère s’en déduit simplement, par projection selon la diagonale.
Le rapport 7
Le carré magique mesure exactement le septième de la largeur de la gravure. Donc la sphère mesure également le septième de la hauteur : autrement dit, horizontalement la gravure est graduée sur la mesure du carré ; et verticalement sur la mesure de la sphère.
L’échelle et la sphère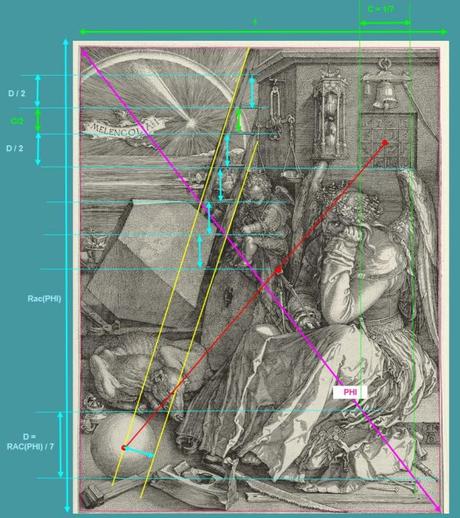
Ses sept barreaux font peut être allusion à la mesure de la gravure (sept carrés sur sept sphères). Mais l’échelle entretient avec la sphère un rapport géométrique particulier : en prolongeant vers le bas le bord extérieur des montants, on voit qu’ils encadrent exactement le rayon de la sphère. De même, verticalement, l’espacement entre les barreaux est lui aussi égal à ce rayon :
en quelque sorte, l’échelle est « posée » sur la sphère, et construite selon sa mesure.
L’instrument de la solution
Si le compas et la règle échouent à résoudre la quadrature, l’échelle serait-elle l’instrument adéquat ? Nous avons dit que ses barreaux sont espacés d’un rayon de la sphère : c’est vrai pour ceux du bas. Puis subitement, entre le cinquième et le sixième barreau, l’espacement diminue, prenant subitement la mesure du carré. Ensuite, entre le sixième et le septième barreau, l’espacement redevient normal.
Monter l’échelle
Les esprits prosaïques diront que cette irrégularité prouve juste que Durer a eu du mal pour caser ses sept barreaux. Mais remarquons que l’espacement irrégulier ne se situe pas n’importe où : il est à l’endroit le plus remarquable, là où l’arc-en-ciel vient traverser l’échelle, là où le météore apparaît dans le ciel.
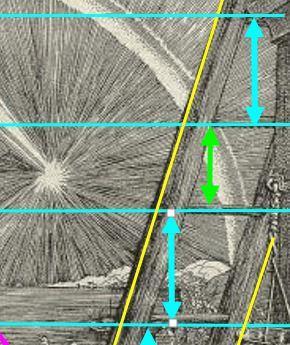
L’échelle ne serait-il pas le véritable instrument dont Melencolia a besoin pour résoudre le problème de la quadrature ? Partant de la sphère, il s’agit de monter les degrés et, subitement, arrivé au cinquième, l’arc-en-ciel illumine le ciel et l’irruption du météore contracte l’espace, à la mesure du carré.
La sphère mesure le septième de la hauteur de la gravure, le carré le septième de sa largeur : ces deux objets donnent en quelque sorte l’étalon de chaque axe. Comme la hauteur est dans un rapport de Racine(PHI) avec la largeur, sphère et carré sont également dans le même rapport, qui est une très bonne approximation du rapport de quadrature périmétrique.
La sphère et le carré sont liés l’un à l’autre par deux contraintes géométriques :
- leur taille relative se construit, comme nous l’avons vu, par une projection selon la diagonale descendante ;
- quant à leurs centres , ils sont être alignés de part et d’autre du centre du compas.
Manière magnifique de traduire, graphiquement, ce que Melencolia a en tête : résoudre à l’aide de son compas le problème de la quadrature.
L’échelle, avec son barreau bancal, illustre bien le caractère transcendantal de la résolution de ce problème : c’est l’apparition des deux météores, la comète et l’arc-en-ciel, qui fournit l’illumination.
Bien des auteurs ont suggéré que le thème de la quadrature du cercle pouvait être un de sujets de la gravure. D’autres ont noté la présence du nombre d’or. Mais le fait que la gravure illustre, très précisément, la résolution de la quadrature par le rapport RAC(PHI), n’a pas été relevé jusqu’ici. Il est étonnant que cette construction géométrique, somme toute assez simple, ait pu jusqu’ici à ma connaissance passer inaperçue.
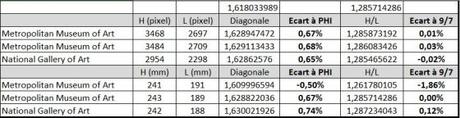
Les valeurs sont extraites de l’étude de Yvo Jacquier, « Dürer et ses tarots« , qui explique bien les difficultés de la mesure, du fait de la variabilité des épreuves. http://www.melencoliai.org/ebook.html
Annexe : Une construction géométrique de la quadrature
Il existe une construction en particulier, qui est basée sur le carré de quatre. Nous n’avons pas de preuve que Durer la connaissait, mais elle donnerait une justification savoureuse à la présence du carré dans la gravure : à la fois énoncé du problème, et épure de sa solution.
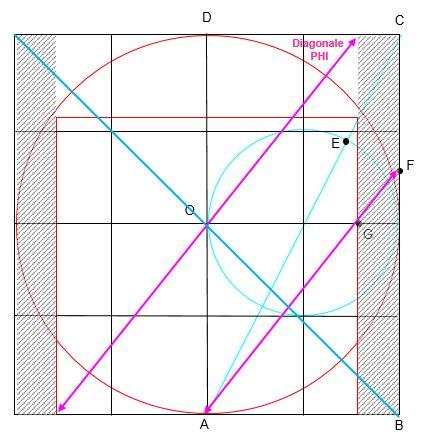
A partir du cercle de rayon R (en rouge) on trace le carré quatre quatre qui l’englobe
On trace le cercle de rayon R/2 (en bleu)
La diagonale AC coupe ce cercle en E
Le cercle de centre A passant par E coupe le bord du carré en F
La ligne AF coupe en G l’horizontale passant par le centre O
Le carré passant par G (en rouge) est la solution de la quadrature du cercle R
Démonstration :
Supposons AB=1. Alors AC= Rac(5). AE=AC/2+AB/2=(Rac(5)+1)/2 = Phi.
Par construction, AF=AE=PHI. Dans le triangle ABF, la base vaut 1 et l’hypothénuse PHI. La hauteur BF vaut donc RAC(PHI).
Thalès : AF/AG=BF/1 => PHI/AG = RAC(PHI) => AG=RAC(PHI).
Le triangle AOG a une hauteur OA de 1 et une hypothénuse AG de RAC(PHI) => le coté OG vaut 1/RAC(PHI)
Le périmètre du carré vaut 8OG = 8/RAC(PHI). Le périmètre du cercle vaut 2PI.
Comme RAC(PHI)=4/PI, les deux périmètres sont égaux
Jeu de briques
Snake
Pacman
Bubble