Contraintes logiques sur les trous de ver et les portes spatio-temporelles

Que ce soit via le film Stargate ou Interstellar (ce dernier étant nettement meilleur), nous sommes devenus familiers avec les trous de ver, ces raccourcis de l'espace-temps qui connectent un région de l'espace à une autre région très éloignée. Physiquement, il en effet possible théoriquement (selon les équations de la relativité générale) de concevoir deux trous noirs qui seraient connectés entre eux pour former... un trou de ver.  toutefois la réalisation pratique d'un tel "tunnel dans l'espace-temps" nécessite apparemment une énergie fabuleuse (supérieure à celle émise par le soleil tout entier durant toute sa vie !), que nous sommes très loin de savoir produire. 

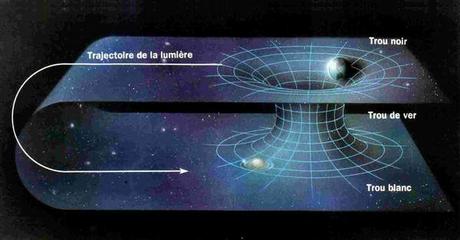
Mais il existe peut-être une solution plus économe !
Mon approche ne consiste pas à torturer les équations pour en extraire une solution possible, mais à examiner les contraintes logiques qui s'appliquent aux trous de ver. L'idée est de se dire : "Supposons qu'un trou de ver puisse être créé, au moyen d'une machine raisonnablement grosse et consommant une énergie raisonnable : alors à quoi devrait ressembler ce trou de ver, et peut-on en créer n'importe où et n'importe comment ?"  La réponse est évidemment non. Il existe des contraintes sur ce que peut, ou ne peut pas être, un tel trou de ver. Et, qui sait, j'ai bon espoir qu'un système physique (une machine)  qui respecterait toutes ces contraintes en créerait automatiquement un !
Qu'entend-t-on par contrainte logique ? Il s'agit des règles "de bon sens" qu'un trou de ver devrait respecter pour exister.  J'ai découvert avec surprise que ces règles sont nombreuses, mais pas insurmontables.

Contrainte numéro 1 : intégrité quantique et continuité

Pour avoir une utilité pratique, un trou de ver (ou une porte de l'espace-temps) ne devrait pas détruire ce qui y pénètre :  Si nous pénétrons dans une telle porte et que nous en ressortons sous forme de bouillie informe ou de plasma, elle n'aura aucune utilité. En fait, une telle porte doit permettre à un corps qui y pénètre de ressortir dans le même état à la porte d'arrivée. Quand nous parlons d'état,  nous parlons d'état quantique, c'est à dire l'arrangement de tous les atomes et particules qui composent le corps d'entrée, ainsi que de la quantité de mouvement (relative) de ces particules.  Nous pouvons reformuler cette contrainte ainsi :
Tout objet qui pénètre dans un trou de ver "utile" doit en ressortir dans le même état quantique.
En particulier un trou de ver "de largeur nulle" ne peut être utilisé pour y passer un objet matériel. Il pourrait en revanche être utilisé pour réaliser des communications instantanées en y faisant passer des photons. Mais nous avons un problème car cela reviendrait à pouvoir définir un temps absolu, or nous savons par la relativité restreinte que le temps est relatif. Nous reviendrons sur ce problème plus tard.
Remarque: il n'est pas forcément nécessaire qu'un objet pénétrant dans le trou de ver en ressorte à l'identique ; il suffit que l'on puisse le reconstituer à l'identique à l'arrivée ! Une forme "affaiblie" de cette contrainte pourrait ainsi être formulée sous la forme suivante, plus générale : Un trou de ver doit préserver  l'information, y compris l'information quantique.

Contrainte numéro 2 : symétrie 

Si un objet O rentre dans la "porte d'entrée" A d'un trou de ver, et en ressort par la porte de sortie B, on doit pouvoir aussi le faire repasser par la porte B pour revenir en A. Le passage d'une telle porte est ainsi bi-directionnel.
 Un trou de ver doit être symétrique et bi-directionnel.

Contrainte numéro 3 : conservation de l'énergie (première forme)

La première contrainte est celle de la conservation de l'énergie.  On peut la formuler ainsi : Aucun trou de ver ne doit permettre de créer (ou de faire disparaître) spontanément de l'énergie. Imaginons une "porte spatio-temporelle". Elle ressemblerait à une porte ordinaire, mais si on la franchit on se retrouverait instantanément à la sortie d'une autre porte, située des kilomètres (ou des années-lumières !) plus loin. Si nous connections deux de ces portes, situées l'une en bas d'une montagne, et l'autre au sommet, nous pourrions alors réaliser un mouvement perpétuel, et extraire de l'énergie à partir de rien : une chute d'eau, par exemple, tombant du haut de la montagne, aboutirait dans la porte inférieure et l'eau se retrouverait automatiquement au sommet pour recommencer le cycle ! Le principe de conservation de l'énergie dit que cela est impossible. Donc nous pouvons formuler plus précisément la contrainte :
Tout trou de ver ne peut relier que des régions de l'espace ayant même potentiel gravitationnel local.
Cette contrainte interdit par exemple de relier deux "portes" situées l'une au fond des mers et l'autre en surface, pour exploiter la différence de pression.
Ce qui s'applique à la gravitation peut également s'appliquer au champ électrique : Si la porte de départ est située près d'un corps chargé positivement, et si la porte d'arrivée est située très prés d'un corps  chargé négativement, on pourrait créer une source d'énergie gratuite en exploitant cette différence de potentiel électrique. Là encore, nous nous interdisons cette possibilité à cause du principe de conservation de l'énergie :
Tout trou de ver ne peut relier que des régions de l'espace ayant même potentiel électromagnétique local.
Nous allons voir cependant avec la contrainte suivante que ce n'est pas si simple !

Contrainte numéro 4 : vitesses relatives compensant la différence de gravitation

Si les deux extrémités d'un trou de ver ont des vitesses différentes, il devient possible d'extraire de l'énergie de cette différence de vitesse. Par exemple si l'extrémité A se trouve sur Terre, au niveau du sol, et l'extrémité B dans une station spatiale en orbite,  on pourrait satelliser n'importe quel objet sans dépenser d'énergie et même récupérer de l'énergie en faisant revenir l'objet sur terre par voie conventionnelle. Le principe de conservation de l'énergie interdit cela.  Donc nous pouvons dire :
Les deux extrémités d'un trou de ver doivent avoir une vitesse relative nulle
Cependant le problème est plus complexe :  En effet la seule chose que nous nous interdisons réellement, c'est de pouvoir créer ou détruire spontanément de l'énergie ou de l'information.  Une manière d'y parvenir est certes de ne relier que des points ayant même gravité, champ électrique et des vitesses relatives nulle ; mais on peut aussi imaginer une porte A située dans un train ayant une vitesse v, et une porte B, stationnaire, située à 1km d'altitude, et s'arranger pour que le gain d'énergie potentielle dû à la différence d'altitude des deux portes soit compensé par la perte d'énergie cinétique dû au fait qu'un "voyageur" allant de A vers B passera de la vitesse v à une vitesse nulle (par rapport à un référentiel lié au sol). De même un voyageur allant de B vers A perdra de l'altitude (donc de l'énergie potentielle), mais gagnera exactement la même énergie cinétique en se retrouvant dans le train à la vitesse v :
mgh = mv² donc v = racine(gh) = racine(9.81  x 1000) = 99 m/s
Ainsi des trous de ver peuvent relier des points de potentiel gravitationnel différents, et de vitesses différentes ! Mais les différences d'énergie doivent se compenser.
Remarquons que du fait de l'expansion de l'univers, les galaxies lointaines s'éloignent de nous à très grande vitesse, et que donc si nous voulons créer un trou de ver pour nous y rendre, nous devons aussi faire en sorte que la porte d'arrivée soit soumise à un champ de gravitation intense...

Contrainte numéro 5 : courbure de la porte

Quelle "forme" aurait (dans notre espace-temps) l'ouverture d'un trou de ver ou celle d'une "porte" spatio-temporelle ? Il y des choses évidentes : sa surface ne doit pas être nulle, et la porte ne doit pas être réduite à un point.  Dans la science-fiction, on trouve des portes en forme de disque (Stargate) ou de sphère (Interstellar).  Le disque a un avantage, c'est qu'il est plan : ainsi on entre dans la porte en traversant un plan, on en ressort en traversant un autre plan :
A ->|.... ....| -> B.
Si on courbe légèrement cette surface (qui devient une portion de sphère, ou de cylindre), alors la courbure "de l'autre coté" doit être symétrique : on entre en A, ressort en B et vice-versa :  A ->)....   ....) -> B.    ou    A ->(....  ....( -> B.
mais on ne peut pas avoir A ->(....    ....) -> B  car dans ce cas un cube (par exemple) entrant en A se retrouvera avec une forme bizarre en  B ! Si nous entrons entrant par une porte convexe, il faut ressortir d'une porte concave ! En d'autres termes,  nous avons la contrainte suivante :
   Les courbures des deux portes doivent être opposées.
Si la porte est une sphère (comme la plupart des trous de vers théoriques ou comme dans le (génial) film Interstellar,  en pénétrant dans la sphère on ne pourrait donc pas ressortir par une autre sphère !

 Dans le film Interstellar on ne voit pas le problème parce que le vaisseau est minuscule par rapport au trou de ver (qui est donc localement plan), mais si le vaisseau avait une taille égale à la moitié de celle du trou de ver,  on verrait bien qu'en entrant dans une surface convexe, il faut ressortir par une surface concave ! On peut s'en sortir en disant que l'univers tout entier (sa copie en fait) se trouve aussi à l'intérieur de la sphère avec une géométrie "inversée" (mathématiquement, une géométrie hyperbolique), le centre de la sphère (que l'on ne peut pas atteindre) correspondant au "bord" de l'univers extérieur (que l'on ne peut pas atteindre non plus d'ailleurs). Nous sommes en pleine spéculation, mais rien ne l'interdit théoriquement !

Contrainte numéro 6 : pas de violation de la causalité

Différent physiciens ont tenté de démontrer que les trous de ver sont impossibles parce qu'ils violeraient le principe de causalité (selon lequel les causes doivent précéder les effets) et qu'ils permettraient de réaliser des voyages dans le temps ! Qu'en est il réellement ?
La proposition d’une machine à voyager dans le temps qui utiliserait un trou de ver, fonctionnerait (hypothétiquement) de la manière suivante : on crée d'une certaine manière un trou de ver, puis, une extrémité du tunnel est accélérée à une vitesse proche de celle de la lumière (peut-être avec un navire spatial d’avant-garde) et on retourne alors au point d'origine.
Étant donné la dilatation temporelle due à la théorie de la relativité restreinte, l'extrémité accélérée du tunnel a vieilli moins vite que l'extrémité stationnaire (du point de vue d'un observateur externe).
Toutefois, le temps à l'intérieur du tunnel est différent de celui qui est en dehors de lui : deux horloges synchronisées postées à chaque extrémité du tunnel se maintiendront toujours synchronisées, du point de vue d'un observateur dans le tunnel, peu importe la différence de vitesse.
Ceci signifie qu'un observateur qui entrerait à l'extrémité accélérée, sortirait par l'extrémité stationnaire quand l'extrémité stationnaire avait le même âge que l'extrémité accélérée au moment avant d'entrer (vous avez une aspirine ?) Par exemple, si avant d'entrer dans le trou de ver l'observateur a remarqué que l'horloge dans l'extrémité accélérée montrait 2015 tandis que l'horloge dans l'extrémité stationnaire disait déjà 2016, alors l'observateur pourrait sortir par l'extrémité stationnaire quand l'horloge stationnaire disait encore 2015. Une limitation significative d'une telle machine est qu'il est  possible de voyager vers le passé en créant un trou de ver, mais pas plus loin que quand la machine a été crée.
Ceci peut permettre une explication alternative au paradoxe de Hawking (si une machine temporelle était possible, nous devrions voir des visiteurs du futur, or nous n'en voyons pas) : un jour on pourra construire une de ces machines, mais comme elles n'ont pas été encore construites, ceci explique pourquoi les touristes temporels ne pourront jamais arriver jusqu’à notre présent actuel.
Cependant à cause de la contrainte numéro 4, si l'extrémité B du trou de ver se déplace à une vitesse très élevée (proche de celle de la lumière), cela signifie aussi qu'elle doit être soumise à un champ de gravitation gigantesque, lequel tuerait certainement tout voyageur (ou détruirait tout dispositif mécanique), ce qui limite en pratique les possibilités de voyage dans le temps !
Un trou de ver est toutefois équivalent à un voyage spatial quasi instantané, donc plus rapide que la lumière. Or nous savons que le temps est relatif, ce qui signifie que la durée mesurée dans un référentiel donné entre deux évènements A et B aura une valeur différentes dans un autre référentiel si ce dernier est en mouvement par rapport au premier (voir l'article relativité sur ce site).
On peut démontrer que, si on peut transmettre des signaux plus vite que la lumière, alors il existe un référentiel (en mouvement), dans lequel un évènement donné pourrait exister avant l'évènement qui en est la cause dans d'autre référentiels.   En fait pour effectuer une vraie violation de causalité, nous devons considérer deux trous de vers : un premier reliant A et B (immobiles dans un certain référentiel), et un second reliant C et D  ; Imaginons que C et D sont en mouvement (très rapide) par rapport à A et B. Imaginons encore qu'à un moment donné A et D soient très proches l'un de l'autre, et B et C aussi : (dans le schéma ci-dessous,  les pointillés ........ représentent les trous de ver)
A |...........................................| B
   C|...............................................|D   
(le référentiel C,D se déplace très vite par rapport à A et B)
                 
De telle sorte que Alice (située en A)  envoie par son trou de ver un message "instantané" à Bob situé en B, lequel peut alors passer (par radio ordinaire) le message à Daniel (situé en D), lequel envoie à son tour (par son trou de vers D->C) le message à Carole (situé en C) ;  Carole envoie alors le message (par radio) à Alice.  Le truc incroyable (mais que l'on peut prouver) est que Alice recevra le message de Carole avant même de l'avoir envoyé à Bob ! Il y a clairement violation de causalité dans ce scénario.
Toutefois, même en acceptant la possibilité des trous de ver ou des portes spatio-temporelles (ce qui est l'hypothèse de départ de cet article), il n'est pas certain qu'un tel scénario soit possible. En effet  selon les contraintes 3 et 4, aussi bien (A et C) que (B et D) devraient se trouver dans des champs de gravitation très différents, donc loin l'un de l'autre. Si l'on ne veut pas de violation de causalité (et on n'en veut pas !), il faut que cette distance obligatoire soit telle que le délai de transmission par radio soit suffisant pour annuler le paradoxe apparent.  Je vous laisse méditer là dessus...

Les coordonnées d'arrivée

Pour finir, je voudrais citer un aspect important des trous de vers tels qu'ils sont décrits dans la science-fiction : dans Stargate, un trou de ver ne peut exister qu'entre des "portes" qui doivent avoir été préalalablement construites. Dans le roman "L'étoile de Pandore" de  Peter F. Hamilton, il suffit de construire une extrémité du trou de ver avec la machinerie adéquate, et on peut créer de toutes pièces un trou de ver vers n'importe quel point de l'univers (pas trop lointain)  en "calculant ses coordonnées".  On peut même déplacer comme on veut l'extrémité "libre" du trou de ver ! Nous avons vu que cela n'est pas si simple et qu'il faut respecter en réalité quelques contraintes.... Mais comment au juste établir un trou de ver entre deux points précis de l'espace ? Comment "dire" à la machine située en A que c'est le point B qu'il faut viser ? La relativité nous dit qu'il n'existe pas de système de coordonnées absolu.  Peut-on déterminer une région de l'espace par sa "signature quantique" ? Cette question me passionne. Si vous avez des idées...
Partagez / votez pour cette page :