Le pouvoir de l' imaginaire (378) censuree modifiee

Espérant ne pas avoir trop découragé mes lecteurs sur les imperfections des mathématiques   et sur les prédictions à faire concernant leurs développement  , je me résignais à vous suggérer  un Avenir tourné vers l’informatique   lorsque mon  CANDIDE   s’est  brusquement  étonné  d’une telle  proposition ……( Si quelqu un est déjà boiteux  pourquoi le faire  courir plus vite ? DIT  IL !)

------------------------------------------------------------------------------------------------------------

-« Je m’insurge  PAPY ! Puisque tu me rappelles sans arrêt que les maths marchent avec les béquilles   décelées par GODEL   déjà pour l’ arithmétique  de PEANO  (= « on ne peut démontrer pour tout système formel  ,  si telle proposition  est juste ou fausse » >>>>>>> voir ma photo  ) , pourquoi  les  vois-tu  s’ en débarrasser par  l’entrée en scène «  grand format »  de l’informatique ?

-« Tu as raison  PIERRE   de me le rappeler   et je vais même enfoncer  ton clou ! Le théorème de GODEL  datant de 1930  les  jeunes générations de matheux  ont cru qu’ on pouvait  transformer ses béquilles  en  robots cybernétiques : en bref , empiler axiome sur axiome pour  rendre toutes les propositions  de maths décidables…. Cela va te surprendre car   on  prétendait  même  aller chercher  dans   le MONDE  REEL   la solution  (dans la théorie de l’information de  A.KOLMOGOROV et  par une complétion algorithmique d’axiomes)….. Et c’est le russo-américain  LEONID LEVIN   qui en a  rajouté en 1971 en démontrant tout  le contraire  ….

-«   N’était-ce pas  évident  intuitivement  PAPY !?A priori l’idée était stupide !  Si je perds ma jambe et prends une béquille à sa place   , ce n’est pas une « robotisation »  de celle-ci   QUI FERA REPOUSSER MA JAMBE !

-«  Et bien c’est précisément ce que L.LEVIN  a démontré : je ne peux  PIERRE   t’expliquer même en version « allégée »  ses théorèmes  mais  je vais essayer d’être clair et en même temps philosophe ( ce que toi tu considères comme contradictoire !) :

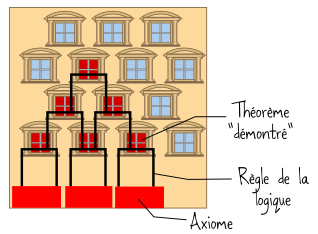
1) Inutile d’ajouter des axiomes pour «  contourner »  GODEL  ( même aléatoirement ou  interminablement ETC   ) et construire un « MEGA PROGRAMME ».

2)Le système  devient  si « lourd »  qu’ il porte une information infinie    

3) On tombe alors   sur la théorie de la calculabilité  de  ALAN TURING ( = « une suite peut être mathématiquement parfaitement définie  et pourtant non calculable par un algorithme   par suite du problème de l’arrêt »)

-«  Et alors on  range   l’arithmétique de PEANO  ou la théorie des ensembles   au placard  PAPY , ?

-«  Non ! ON SE RESIGNE ! D’après  LEONID LEVIN  et les logiciens actuels cela va beaucoup plus loin que cela , PIERRE…. JE CITE L’ARTICLE DE Jean- Paul  DELAHAYE   ; il y aurait  séparation des deux mondes : «  ce postulat d’indépendance entre processus physiques  et informations mathématiques  est une loi   de  conservation de l’information : certaines informations ne sont pas dans le monde physique et ne peuvent y être produites  .Ce postulat ….fixerait des limites définitives aux informations qu’on pourra extraire du monde physique    .IL SERAIT EN QUELQUE SORTE LA RAISON PROFONDE DU PHENOMENE D INCOMPLETUDE QUI CONCERNERAIT NON SEULEMENT  LES MATHEMATIQUES MAIS AUSSI LA PHYSIQUE »

-«   Sans blague PAPY  , tu deviendrais encore plus «  aquoiboniste » que moi !......je   devrais commencer par te demander de m’expliquer  ce qu’ est un algorithme  et comment on s’en sert pour bâtir des logiciels  ET  ATTAQUER LA RESOLUTION DE PROBLEMES DE MATHEMATIQUES AVEC …EST-CE POSSIBLE ? En –as –tu fait ?

-« J’ai fait faire de sévères calculs en  FORTRAN   par des collaborateurs ingénieurs  dans le cadre d’études de séparation isotopique uranium  et pour le lancement des usines Eurodif …..  Pour mon malheur,  j’ai dû moi-même  me mettre  au  système d'exploitation PC-DOS développé par Microsoft pour l'IBM PC, ainsi que la variante MS-DOS vendue par Microsoft pour les compatibles PC.  Ce système en ligne de commande était rudimentaire : pas de multitâche, pas de mémoire virtuelle, Etc.   Pour les études de sécurité  nucléaire  nous avons utilisé  un mode informatique  que je ne puis révéler.   MA réponse  à tes questions sera mon prochain article !

 A suivre