Attention ! Nous quittons peu à peu le domaine de notre concret familier… Peut-être quelque philosophe de notre blogosphère va-t-il nous rejoindre… ?
-----------------------------------------------------------------------
-« Je me suis aperçu PIERRE que tu n’avais peut-être pas suffisamment perçu que passer du nombre entier au nombre fractionnaire , c’était déjà faire un saut dans une catégorie d’abstrait plus complexe ….
-« Ah bon ! Qu’est-ce que j’ai encore raté PAPY… ?
-« Rien ! Tu me proposes trop vite l’abstrait mathématique grec antique ! Les égyptiens anciens ont utilisé les nombres fractionnaires et les nombres non entiers dans des tas de cas…. Mais s’ils ont fait de l’analyse opérationnelle « rustique » et déduit de bonnes recettes de calcul , on ne peut dénier aux sciences égyptiennes toute conceptualisation ;il en manque simplement les traces …… En fait la nouveauté des mathématiques grecques, c ‘est qu’elles , elles deviennent une branche de la philosophie.
-« Et vlan PAPY ! NOUS TOMBONS ALORS DANS LE PETIT BOUT D’ABSTRAIT QUI T’ INTERESSE !
-« Oui ! Et doublement car de l'argumentation philosophique ( la Logique) découle l'argumentation mathématique. Il ne suffit plus d'appliquer, il faut prouver et convaincre : c'est donc la naissance de la démonstration. Mais surtout au lieu de travailler sur des méthodes opérationnelles ,( savoir tailler des pierres ,en faire des pyramides , calculer surfaces et volumes etc. ) les mathématiques grecques se mettent à étudier des représentations parfaites d'objets réels : on ne travaille plus PIERRE sur un cercle « malfoutu » mais sur l'idée d'un cercle et on découvre ( avec ravissement ) les propriétés qui en découlent !
-« Et nous nageons alors dans l’imaginaire donc dans l’abstrait !Là je te comprends PAPY !
-« Je ne t’ai pas tout dit ! Selon l'école pythagoricienne, « tout est nombre ». Mais leur souci d’idéaliser les nombres en les associant à des considérations géométriques les conduit à n'accepter d'abord comme nombres que les nombres rationnels pour lesquels il doit exister une unité dans laquelle deux longueurs seront entières. Cette sélection les conduit DANS UNE IMPASSE ! Que devient racine de 2 ? Ils vont n'accepter que les nombres constructibles à la règle et au compas et se heurter alors aux trois problèmes qui vont traverser les siècles : la quadrature du cercle, la trisection de l'angle et la duplication du cube. ! ( voir ma photo ci dessous sur la duplication du carré par l’esclave de SOCRATE )
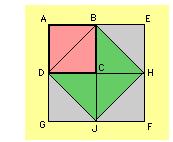
DIEU merci , il y a eu EUCLIDE ! La synthèse la plus importante des mathématiques vient de ses Éléments …. C est la première formalisation de la pensée mathématique. Il définit les objets géométriques (droites, cercles, angles), il définit l'espace par une série d'axiomes, il démontre par implication les propriétés qui en découlent et fait le lien formel entre nombre et longueur…..Mais nous en verrons plus tard les limites ……. C’est la formalisation la plus stricte que permettait le langage , la sémantique et la symbolique de l’époque ……
-« Et alors ? Et après ?
-« Il faut rester lucide PIERRE sur les marches historiques discontinues du progrès humain … Les êtres humains ont préféré pendant des temps immémoriaux continuer à engendrer des mythes ( voir l’article de l anthropologue JULIEN D HUY ( POUR LA SCIENCE AOUT 2014) et cultiver des religions et des croyances ! .En matière d’abstraction mathématique et de développement de la symbolique adéquate , pour moi il a fallu attendre l’invention du zéro , les chiffres arabes et l algébre , autrement dit la Renaissance !
A suivre
