Partager la publication "Test d’hypothèse ou l’analyse statistique des tests A/B"

Optimisation du taux de conversion d’une Landing Page
Supposons que vous testiez une landing page qui intègre un formulaire d’inscription. Vous voulez expérimenter différentes mises en page pour essayer de maximiser le pourcentage de personnes qui s’inscrivent, autrement dit optimiser le taux de conversion du formulaire d’inscription.
Vous avez quatre pistes d’expérimentation, une version de contrôle et trois versions expérimentales.
Pour cette expérience, nous allons simplement appeler les versions, A (contrôle), B, C et D.
Les données
Votre Projet X est génial, vos efforts marketing attirent les utilisateurs. Vous avez analysé votre tunnel de vente et les points de contact qui ont le plus d’impact sur la conversion, telle que la landing page. Justement, vous souhaitez augmenter son taux de conversion d’au moins 20%.
Vous créez un test A / B avec quatre versions : A (contrôle), B, C et D. Voici les données que vous collectez:
Project X Landing Page
Versions Visiteurs version Visiteurs convertis Conversion Rate
A (Control) 182 35 19.23%
B 180 45 25.00%
C 189 28 14.81%
D 188 61 32.45%
D’après les données les versions B et D montrent au moins une amélioration de 20% de la performance de la landing page, ce qui était notre objectif. Vous pouvez déclarer la version D « suffisamment bonne », la choisir, et passer à autre chose. Mais comment savez-vous que la variation n’est pas due au hasard aléatoire? Et si au lieu de 188 visiteurs nous n’avions que 10 visiteurs de la version ? Seriez-vous toujours si confiant ?
Comme d’habitude, nous visons un intervalle de confiance de 95%.
Le test d’hypothèse est l’outil qu’il nous faut pour quantifier notre confiance statistique.
En statistiques, un test d’hypothèse est une démarche consistant à rejeter ou à accepter une hypothèse statistique, appelée hypothèse nulle (H0), en fonction d’un jeu de données (échantillon).
Nous avons besoin pour initier notre test d’hypothèse d’une hypothèse nulle. Dans notre cas, l’hypothèse nulle sera que le taux de conversion de la version A (contrôle) n’est pas inférieur que le taux de conversion de la version D. Mathématiquement
H0 : p – pc ≤ 0
Pc est le taux de conversion de A (contrôle) et p est le taux de conversion de l’une de nos versions.
L’hypothèse alternative est donc que la version expérimentale qui a le taux de conversion le plus élevé. C’est ce que nous voulons vérifier et à quantifier.
Les taux de conversion sont échantillonnés en variables aléatoires normalement distribuées (Loi normale) pour vérifier les écarts entre la version de contrôle (A) et la version expérimentale.
Voici un exemple de représentation de la distribution normale des taux de conversion de la version A (contrôle) et de la version D.
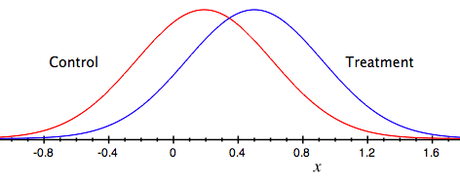
Le sommet de chaque courbe représente le taux de conversion que nous mesurons, mais il y a des chances qu’il soit en réalité quelque part ailleurs sur la courbe. En outre, ce qui nous intéresse vraiment est la différence entre les deux taux de conversion. Si la différence est assez grande, nous pourrons conclure que la version a vraiment optimisé le taux de conversion.
Donc, nous allons définir une nouvelle variable aléatoire
X = p – pc
alors notre hypothèse nulle est
H0 : X ≤ 0
Nous pouvons maintenant utiliser les mêmes techniques que pour le Pile ou Face, en utilisant la variable d’aléatoire X. Mais pour ce faire nous avons besoin de connaître la distribution de probabilité de X.
Il s’avère que la somme (ou la différence) de deux variables aléatoires normalement distribuées est elle-même une distribution normale.
Cela nous donne un moyen de calculer un intervalle de confiance de 95%.
Z-scores et des tests unilatéraux
Mathématiquement, le z-score pour X est
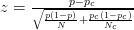
où N est la taille de l’échantillon de la version expérimentale D et Nc est la taille de l’échantillon de la version A (contrôle).
Pourquoi ? Parce que la moyenne de X est p – pc et la variance est la somme des variances des p et pc.
Nous rejetons l’hypothèse nulle si le taux de conversion de la version expérimentale D est significativement plus élevé que le taux de conversion de la version de controle A, nous avons donc
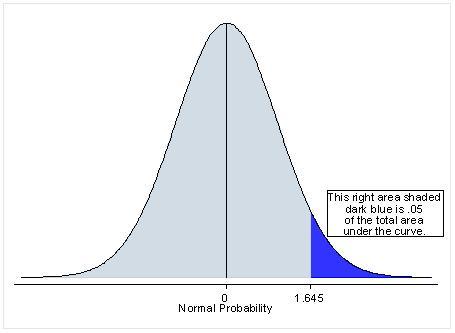
Autrement dit, on peut rejeter l’hypothèse nulle avec une confiance de 95% si le z-score est supérieur à 1,65. Voici un tableau avec les z-scores calculés en utilisant la formule ci-dessus:
Project X Landing Page
Version Visiteurs version Visiteurs convertis Conversion Rate Z-score
A (Contrôle) 182 35 19.23% N/A
B 180 45 25.00% 1.33
C 189 28 14.81% -1.13
D 188 61 32.45% 2.94
Conclusions
Dans le tableau ci-dessus, nous sommes sûrs de conclure que la version D a fait mieux que la version de contrôle A. Si la performance de la version B est statistiquement significative, mais pas suffisamment pour surpasser la version D, qui doit être sélectionnée pour remplacer la version de contrôle avant de procéder à de nouveaux tests A/B.
Voici les principaux enseignements :
- Le taux de conversion de chaque version est une variable aléatoire à distribution normale
- Nous voulons mesurer la différence de performance entre une version donnée et la version de contrôle.
- La différence elle-même est une variable aléatoire à distribution normale.
- Pour notre sujet, si la différence est supérieure à zéro, nous avons seulement besoin d’un z-score de 1,65, ce qui correspond à la moitié positive de la courbe normale.
La confiance statistique est importante pour les tests A/B, car il nous permet de savoir si nous avons exécuté le test pendant assez longtemps. En fait, nous pouvons poser la question inverse, « Combien de temps ai-je besoin pour exécuter un test avant d’être certain qu’une de mes versions fasse plus de 20% que la version de contrôle ? »
source http://20bits.com/article/statistical-analysis-and-ab-testing
Partager la publication "Test d’hypothèse ou l’analyse statistique des tests A/B"






