Le pouvoir de l' imaginaire (357)

Continuons  nos  interviews  fictifs  entre  PIERRE  et moi !

-« Je suis au regret de te dire PAPY  , que concernant  ce continent gravitationnel galactique nouveau   que tes amis ont appelé LANIAKEA , je ne vois guère comment mener un « calcul de coin de table »  comme tu me l’ assures !Par conséquent peux-tu justifier  la figure que tu nous as présentée ?

-« Pierre , je vais te demander alors quelques efforts de raisonnement mathématique et te présenter des graphiques ….Quant à me justifier  d’un modèle de calcul simplifié et plutôt intuitif, il n’en est pas question :je t’ai déjà dit qu’ il était merveilleux de laisser  jaillir et déborder  ses idées  quitte à sortir presque aussi vite sa gomme de sa poche !

Et pour commencer je te propose  de poser le problème  d’une galaxie qui se trouve sur le bord de  LANIAKEA . Supposons qu’ il s’agisse  d’une galaxie « spirale plan » de type « Voie lactée » de masse   M₀  et  qui contient, selon les derniers relevés du télescope spatial Kepler, entre 200 et 400 milliards d’étoiles .Je vais l’appeler  GALAXIE STANDARD ….. SANS CEPENDANT PRENDRE LE RISQUE D’EN EVALUER LA VALEUR MASSIQUE  IMMEDIATEMENT …… Et puis je vais  te demander  au regard de M◦ quelle est la masse attractrice ?

-« Papy , je ne puis que seulement te dire que ce que  l’article   de Daniel Pomarede  et allia   m’a appris :Laniakea Supercluster comprend environ  100000 galaxies  et s ‘étend sur une distance de  160 mégaparsecs (520 millions d’années-lumière ).ma photo 1 de la boule " patatoide" que vous pourriez voir en agrandi sur leur site 

LANIAKEA SUPERCLUSTER 

Map of the nearest superclusters within 500 million light years. Laniakea is the long chain of galaxies which covers the Centaurus Wall and the superclusters Virgo, Hydra, Centaurus and Pavo-Indus at the centerCredit: Richard Powell, Atlas of the Universe website

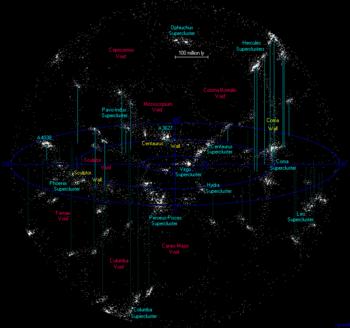
-« Alors puisqu’ on est parti pour une modélisation , supposons  PIERRE  que toute la masse apparente visible de LANIAKEA   soit égale à : M₁=100000 M₀   et évaluons la force de  rappel gravitationnel en prenant  comme distance moyenne d’attraction seulement le rayon du  continent  , soit D (M₀ - M₁)= 260 millions d années lumière

-«ET   ça nous mène où,  tout  ça,  PAPY ?

-« Selon NEWTON   la force d’attraction du continent sur cette galaxie frontière  sera  F( M₁  M₀)  = G .100000 M₀²/  (260. 10↑6)²  et pour l’instant n’allons pas plus loin ( car il y a problème avec l’évaluation de M₀  a cause de la masse « noire ») !

-«   Pourquoi ?

-« Parce que ce qui intéresse mon calcul de coin de table   c’est la  dispute qui va se jouer entre les 2 continents gravitationnels voisins  LANIAKEA  et  SHAPLEY SUPERCLUSTER et c’est cela  qui m’intéresse en priorité , !!!!!

Qui va réussir à s’emparer de notre petite galaxie  M₀   a leur  frontière ??????

-  Pour une fois j’espère pouvoir te répondre  PAPY !  Ce sera celle  qui  exercera la force gravitationnelle la plus forte ! Donc cela dépendra  de la masse  globale de SHAPLEY  ,soit  M2   et de son rayon ,R 2 !Si celle-ci  est  plus forte  ( soit du fait de la valeur de M2  ou plus dense)  , notre petite galaxie standard  se sauvera  comme la chèvre de Mr SEGUIN  sur SHAPLEY …. SINON  elle continuera à remonter vers le centre de  LANIAKEA ……

-"PIERRE !  Traduit mathématiquement  cela devrait donner un jeu d abaques   formidablement complexe car les densités de  LANIAKEA et de  SHAPPLEY  interviennent aussi  et évoluent différemment .   Tu peux donc dresser  le tableau  des divers  cas suivants possibles

 1° :M1>M2 mais D1=D2

2° :M1>M2 mais D1>D2

3° :M1> M2 mais D1<D2 …..

avec  bien entendu le tableau symétrique  pour le cas M1<M2 et tu définis la force de rappel de M2 , F (M2 -M0)   par rapport à la valeur de M0 …..Ce qui exige soit  une connaissance expérimentale mesurée de   SHAPPLEY soit une  hypothèse  d’ évaluation  ….En réalité   LANIAKEA  et SHAPLEY sont très hétérogènes en densité   et les  forces d’attraction  au voisinage de M 0   peuvent aussi  dépendre d’un attracteur local ….

…..Quoiqu’il en soit la deuxième photo te donne alors  une idée  approchée de deux  paysages futurs  possibles   et justifie la photo du graphique présenté dans « LE POUVOIR DE L’IMAGINAIRE  «  n°  356 ……Mais cela devrait surtout  te suggérer PIERRE  un bien plus gros problème  dont nous avons parlé ici dans maints articles …..La photo montre qu  M0 part vers M2 dans le 1 er cas ou vers M 1 dans le 2 ème sauf si  l attracteur local  proche de M2 est plus"puissant" que l attracteur local de M1.....

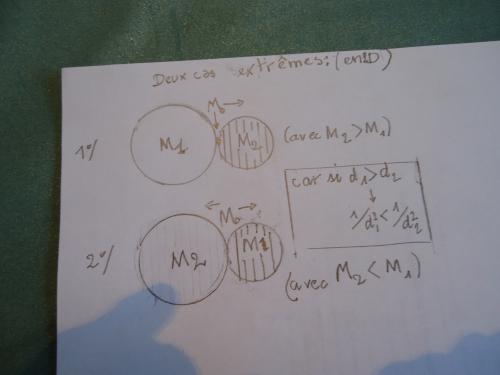
-« Quel  plus gros problème ?

-«   Il s’agit du célébrissime  « problème des  3 corps gravitationnels »  attaqué  par HENRI   POINCARE  ou  SURTOUT du problème général  encore plus ardu des N  corps compliqué par l’application de la Relativité Générale   ! D’autant que mon modèle n’est qu’une énorme approximation !

 A SUIVRE