Généralités sur les Calculs de doses

La Numération : 

Position et valeur d’un chiffre : 

Pour écrire un nombre, différentes classes sont déterminées :

• la classe des unités simples
• la classe des milliers
• la classe des millions
• la classe des milliards

A chacune de ces classes correspond un redécoupage en tranche de trois chiffres. Au sein de chaque tranche, le chiffre sera soit une unité, soit une dizaine, soit une centaine.

L’écriture Romaine : 

Son utilisation est encore d’actualité dans un soucis de sécurité car elle évite notamment la confusion avec l’écriture en chiffres arabes. On l’utilise pour indiquer le nombre de gouttes buvables.

I = 1

V = 5

X = 10

L = 50

C = 100

D = 500

M = 1000

(Moyen mnémotechnique : Il VeXe Le Commun Des Mortels).

La notation exponentielle (puissances de 10) : 

Exposant positif : 

Pout n entier positif supérieur ou égal à 2,

 est le produit de n facteurs tous égaux à 10.

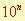
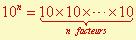
Donc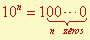 

( 1 suivi de n zéros)

cas particuliers :

 

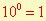
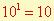
n s’appelle l’exposant.

Exemples :  

 
 

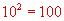
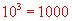
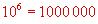
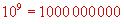
Exposant négatif : 

  
 
 est l’inverse de  .
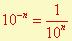
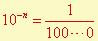
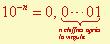
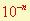
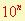
c’est à dire .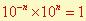

Exemples: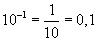

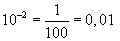
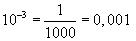
Multiples et sous-multiples des unités fondamentales : 

Ceux-ci permettent de manipuler plus facilement de très grandes ou de très petites unités. Les principales unités utilisée sont :

• Le mètre (m) = unité de longueur
• Le gramme (g) = unité de poids
• Le litre (l) = unité de volume
• Le mole (mol) =  unité de quantité
• La seconde (s) = unité de temps

A chaque unité se rapportent des multiples (plus grands) et des sous-multiples (plus petits) qui correspondent aux puissance de 10 positives ou négatives.

Les unités de mesure : 

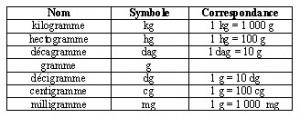
Mesures de masse : 

academie-en-ligne.fr

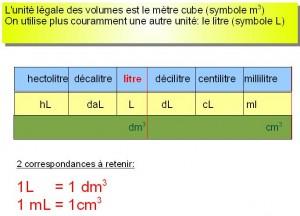
Mesures de volume : 

clg-la-ferte-st-aubin.tice.ac-orleans-tours.fr

Autres types de mesure : 

1 cuillère à café = 5 ml

1 cuillère à dessert = 10 ml

1 cuillère à soupe = 15 ml

1 verre ordinaire = 150 ml

Les équivalences suivantes : volume-nombre de gouttes, en fonction de la solution à préparer, sont indispensables à connaître pour l’infirmière : 

Solution aqueuse : 1 ml = 20 gouttes de solution aqueuse

Sang :  1 ml = 15 gouttes de sang

Les Unités internationales (UI) :

Elles sont utilisées afin de disposer d’un référentiel international commun afin d’éviter les erreurs  du à l’utilisation de données propre aux fabricants et aux laboratoires.

ex : L’héparine se mesure en UI et non plus en mg.

Les Concentrations : 

La concentration c’est la masse dissoute dans l’unité de volume d’une solution. On peut la chiffrer de deux manières :

• En pourcentage (pour cent : %, pour mille %0, pour dix mille %00)
• En poids par unité de volume (g/l, mg/l, g/100ml, mg/ml etc…)

Il est très important de comprendre à quoi cela correspond pour bien appréhender les calculs de dose.

% correspond à : gramme pour cent millilitre

Exemple : une ampoule de NaCl de 10 ml à 20 % contient :

• 20 grammes de NaCl pour 100 millilitres donc,
• 2 grammes de NaCl pour 10 millilitres (réduction de 1 zéro) donc une ampoule de NaCl de 10 ml à 20% contient 2 grammes de NaCl

La règle de trois :

La règle de trois consiste à calculer une inconnue avec trois données.

Dans un premier temps, on effectue une division des deux données aux unités différentes pour obtenir la valeur de la proportion correspondant à une unité de l’inconnue recherchée.

Dans un second temps, il faut multiplier cette proportion par la troisième valeur.

Exemple :

Vous devez injecter 250 mg d’aspirine à un patient et pour cela vous disposez d’un flacon de 500 mg et de 5 ml d’EPPI.

Dans un premier temps : combien de ml représente un mg de produit :

5 / 500 = 0,01 donc 1 mg = 0,01 ml d’aspirine

Dans un second temps, combien de ml représente 250 mg :

250 * 0,01 = 2,5 donc 250 mg d’aspirine est égal à 2,5 ml de solution.

Vous injecterez donc 2,5 ml de solution

Les produits en croix : 

Il s’agit d’une autre technique permettant d’obtenir un résultat à partir de trois données.

La règle utilisé est celle de l’équivalence entre deux fractions :

a / b = c / d

a et c sont les numérateurs et b et d sont les dénominateurs.

On peut alors multiplier le numérateur de la première fraction avec le dénominateur de la seconde fraction et le numérateur de la seconde fraction avec le dénominateur de la première.

a * d = b * c

Si l’inconnue est d on obtient alors :

d = (b * c) / a

Exemple :

20 / 2 = 100 / X

Donc on peut dire : 20 x X = 100 x 2

donc X = (100 x 2) / 20

donc : X = 200 / 20

alors X = 10

Les Débits :

Le débit est le rapport d’un volume sur le temps. Le débit d’une perfusion s’exprime en gouttes par minutes ou en millilitre par heure. Pour le calculer, il faut se souvenir que :

Pour les solutés standard : 1 ml = 20 gouttes

Pour le sang : 1 ml = 15 gouttes

Pédiatrie, microdrip : 1 ml = 60 gouttes

Le temps :

   L’unité de temps est la seconde : s

   Les sous-multiples de la seconde sont :

•   La minute : mn : 1 mn = 60 s
•   L’heure : h : 1 h = 60 mn = 3600 s

La capacité : 

   L’unité de la capacité est le litre : l

   Les sous-multiples du litre sont :

• Le décilitre : dl : 1 dl = 0,1 l   donc   1 l = 10 dl
• Le centilitre : cl : 1 cl = 0,01 l   donc   1l = 100 cl
• Le millilitre : ml : 1 ml = 0,001 l   donc   1l = 1000 ml

Source : http://www.infirmiers.com/etudiants-en-ifsi/cours/cours-transversaux-calcul-de-doses-cours.html

Dominique Rispail, Alain Viaux, Guide du calcul de doses et de débits médicamenteux, Masson, 2007