Pourquoi n’y a-t-il que 5 polyèdres réguliers (convexes) ?

Dans le plan, en dimension 2, il y a une infinité de polygones réguliers : triangle équilatéral, carré, pentagone, hexagone, n-gone (voir dans mon premier ouvrage, p.68-69, l’approximation par Archimède de pi au moyen du périmètre des polygones réguliers inscrits dans le cercle). Or, en dimension 3, dans l’espace, n’existent que cinq polyèdres réguliers convexes (ou solides de Platon — encore un Grec). Pourquoi ? Comment ? De qui, de quoi ? Pour la géométrie, une référence, un guide de voyage : le Berger (Géométrie vivante, Cassini, 2010) — comme une étoile qui nous… guide. Style direct et sans bavures. On en avait déjà eu deux échantillons en 2011 (polygones étoilés et enjoliveurs) et 2009 (cercles du tore) dans ce blog.

Le mage Berger utilise la relation d’Euler, bien connue dès la maternelle (je plaisante à peine : on pourrait la faire toucher du doigt aux enfants avec les cubes de leurs jeux de construction, ou avec les ballons de foot) : S – A + F = 2, où S est le nombre de sommets, A le nombre d’arêtes, F le nombre de faces. Il l’écrit subtilement f₀ – f₁ + f₂ = 2 (où f₀ est le nombre d’entités sans dimension, des points, ou des sommets, S ; f₁ est le nombre d’entités à une dimension, les arêtes, A ; etc.). Gardons la notation classique, et introduisons h le nombre d’arêtes partant de chaque sommet, et k le nombre de sommets par face.

Pour ceux qui veulent toucher du doigt, ou qui veulent des chiffres concrets, voici le tableau pour les 5 polyèdres réguliers convexes :

S

A

F

h

k

Tétraèdre

4

6

4

3

3

Cube

8

12

6

3

4

Octaèdre

6

12

8

4

3

Dodécaèdre

20

30

12

3

5

Icosaèdre

12

30

20

5

3

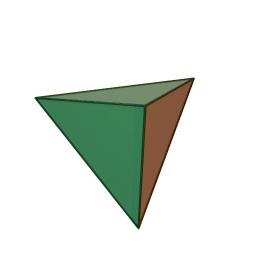
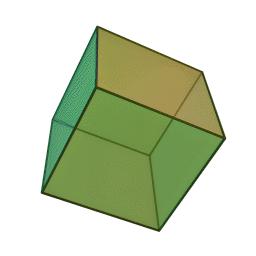
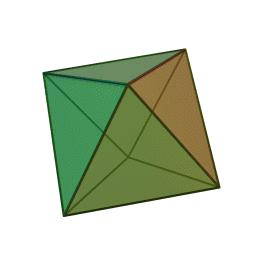
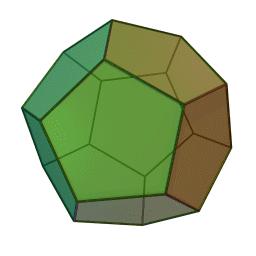
(animations ci-dessus Wikimedia Commons, auteur Cyp, Creative Commons cc-by-sa)

(de haut en bas dans l'ordre du tableau, qui est le nombre croissant de faces)

Un sommet appartient à h faces (pour s’en convaincre, aplatir le voisinage d’un sommet sur un plan : le nombre d’arêtes partant du sommet, h, est égal au nombre de faces qui sont entre ces arêtes). Le nombre total de sommets, S, est donc égal à Fk (nombre de faces × nombre de sommets par face) divisé par h, puisqu’un sommet appartient à h faces (vérifier avec le tableau). Le nombre total d’arêtes, A, est égal à Sh (nombre de sommets × nombre d’arêtes partant de chaque sommet), divisé par 2, puisqu’une arête relie deux sommets (« appartient » à deux sommets).

S = Fk/h

A = Sh/2 = Fk/2

Reprenons la relation d’Euler, S – A + F = 2, et réinjectons ces valeurs.

Fk/h – Fk/2 + F = 2

Fk + Fh = 2h + Fkh/2  > Fkh/2

k + h > kh/2

1/h + 1/k > 1/2

Or, si l’on réfléchit, il y a peu de couples d’entiers {h,k} (strictement supérieurs à 2) vérifiant cette propriété : {3,3} (tétraèdre), {3,4} (cube), {4,3} (octaèdre), {3,5} (dodécaèdre), {5,3} (icosaèdre). À partir de 3,6, on a 1/h + 1/k ≤ 1/2, donc la relation ci-dessus n’est pas vérifiée : le polyèdre n’existe pas.

Terminons avec Berger et sa magnifique phrase, une fois démontré qu'il n'existe que cinq polyèdres au plus : "L'existence sera vue plus bas"! Bon, pour l'existence, en ce qui nous concerne, nous nous contenterons des figures ci-dessus.

À suivre bientôt, sur le même thème.