Géométrie gauloise

Connaissez-vous Bibracte, dans le Morvan ? C’est un très beau musée d’histoire gauloise (au singulier) et gallo-romane. C’est aussi un très beau site archéologique, sur le Mont-Beuvray , au pied duquel se situe le musée. Rien que du point de vue science archéologique et histoire, je mets 3* à ce site méconnu. Mais j’y ai aussi vu un sujet de maths amusant – une construction géométrique au compas. On trouvera d'autres constructions à la régle et au compas sur ce blog, par Descartes (le Gaulois ?), ici.

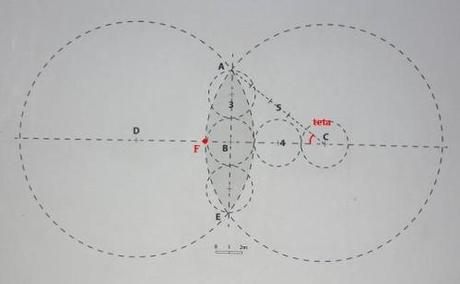
Il s’agit d’un « bassin monumental » datant du 1^er siècle avant J.-C. Comme le précise la notice du site, il est construit avec une unité de 182 cm (environ 6 pieds), qui va correspondre à l’ouverture du compas pour cette construction. On pique le compas en B (ci-dessous), et on l’ouvre à 3 unités pour piquer A dans une direction (en haut sur le schéma) ; puis on l’ouvre à 4 unités pour piquer C à droite et D à gauche. En l’ouvrant à 5 unités, en piquant d’une part en C, d’autre part en D, on repasse par A (théorème de Pythagore). L’intersection de ces deux cercles de centres C et D et de rayon 5 unités trace le bassin, de petit axe égal à 2 unités (3m64) et de grand axe égal à 6 unités (10m92).

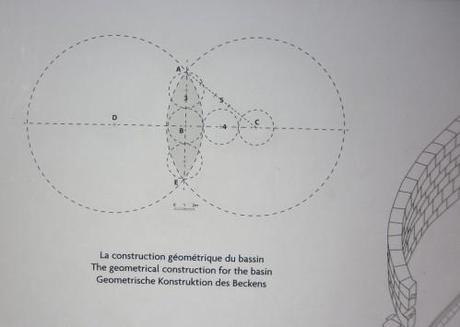
Je ne sais pas comment on appelle cette figure géométrique (ce n’est pas une lunule). On pourra s’amuser à calculer sa surface : le quart de surface ABF est égal à la différence entre la surface AFC interceptée par l’angle θ soit Rθ (R = 5, et tgθ = 3/4) et la surface du triangle 4 × 3 / 2.