Les figures de Lichtenberg: comment la foudre peut tatouer des fractales sur votre peau!

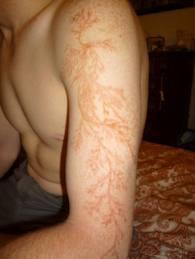
Lichtenberg

La formation des figures de Lichtenberg

LichtenbergGeorg Christoph Lichtenberg
agrégation limitée par diffusionWitten SanderLichtenberg
Todd JohnsonLichtenberg ici

Illustration de la diffusion du sucre dans l'eau

Une sculpture réalisée avec le procédé Captured Lightning®

Figures de Lichtenberg et fractales

Lichtenberg fractalespage interactive

On pourrait croire que les fractales ne sont qu'un amusement mathématique sans lien avec la réalité, mais il s'avère que ces figures sont partout: on les trouve dans les frontières ou les côtes maritimes, le relief terrestre, les bronches, les vaisseaux sanguins, les divisions cellulaires, les cristaux de neige, la foudre (vidéo ci-dessous), les racines, la répartition des galaxies dans l'univers ou mêmes dans des phénomènes a priori sans rapport, comme les fluctuations des crues des fleuves ou celles des cours boursiers.
Bien sûr, dans tous ces exemples, les fractales sont ne sont pas infinies. Néanmoins, la géométrie fractale est le meilleur outil pour le calcul de leurs propriétés. En plus, leurs représentations colorées et géométriques sont d'une beauté fascinante!

Si vous voulez créer votre propre figure de Lichtenberg, rendez vous sur cette page. Vous aurez besoin d'un clou, d'une feuille d’acrylique et d'encre de photocopieur.Vous pouvez aussi consulter celle ci mais cela demande un peu plus de matériel.
Pour en savoir plus sur les figures de Lichtenberg: ce lien en anglais. Et sii vous aimez les maths, lisez ce cours sur les fractales.
Je termine avec une belle image et une dédicace à ma sœur Claire.
 

Une figure fractale, crédits: Evercat, wikipedia commons