Probabilité de la main crève-coeur

Le 17 août dernier, dans un commentaire du billet Le déclin des parties en argent, Pokerman a soulevé la question de la probabilité de la main crève-coeur sur EspaceJeux. Rappelons qu’une main crève-coeur se produit lorsqu’une personne, qui a au moins quatre valets, perd sa mise au profit d’un joueur qui a un carré ou une quinte plus élevés (quinte: une séquence de 5 cartes de la même couleur). Lorsque cet événement se produit, le perdant récolte 50% d’un lot progressif, le gagnant 25% et les autres participants présents à la table se partagent le dernier 25%.

L'obtention de la main crève-coeur exige aussi que les deux cartes cachées des joueurs perdant et gagnant font obligatoirement partie des combinaisons qui s'affrontent.
En théorie, la méthode classique du calcul des probabilités (par exemple, 4/52 x 3/51 x 2/50, etc.) est la plus exacte. En pratique, ce n’est pas vraiment faisable. Tout d’abord, au Texas Holdem, on fabrique la meilleure main de 5 cartes à partir de 7 cartes. L'as va autant avec le deux que le roi. Cela augmente considérablement le répertoire des combinaisons à examiner. C’est si long à faire qu’on s’y perd. Ensuite, cette méthode prend pour acquis que le mécanisme de tirage des cartes est parfaitement aléatoire. Or, ce n’est pas le cas des générateurs de nombres pseudos aléatoires (GNPA). Dès lors, la méthode classique est faussée.

Lorsqu’on ne peut pas calculer la probabilité théorique, on calcule la probabilité empirique. Dans le cas présent, trois mains crève-coeur se sont produites sur le Canadian Poker Network (EspaceJeux + PlayNow) depuis le 1 décembre 2010 (voir tableau suivant). Compte tenu que, à chaque main post-flop, un montant de 35 cents sur 50 est consacré à l’augmentation du lot progressif (c’est écrit en très petits caractères à la fin de cette page), on n’a qu’à diviser le montant du lot remis aux joueurs par 35 cents et on obtient le nombre minimal de mains qui ont été complétées avant que la main crève-coeur ne soit gagnée. À cela, il faudrait ajouter les mains abandonnées pré-flop; ce que je n'ai pas tenté ici.

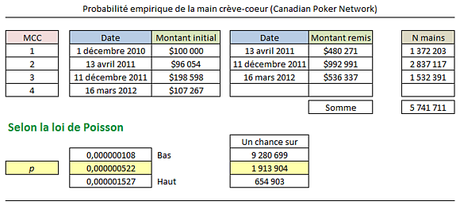
Par exemple, la première main crève-coeur a été gagnée le 13 avril 2011. Un montant de 480.271 dollars a été remis aux joueurs. Entre le 1 décembre 2010 et le 13 avril 2011, il y a donc eu 1.372.203 mains jouées post-flop. Au moment de la troisième main crève-coeur, un total de 5.741.711 mains avaient été complétées depuis le 1 décembre 2010. Cela suggère ainsi que la probabilité de cette main crève-coeur est de ,000000522, c’est-à-dire une chance sur 1.913.904 mains post-flop. Cependant, on ne peut pas dire qu’un estimé basé sur 3 observations procure un résultat vraiment précis. Pour connaître l’intervalle de confiance à 95%, il faut faire un calcul en fonction de la loi de Poisson (en statistiques, c’est en l’honneur du mathématicien Siméon Denis Poisson … aucun rapport avec le poisson du poker). Ce calcul indique une probabilité entre une chance sur 654.903 et 9.280.699. Bref, c’est vraiment imprécis.

Une autre solution est d’y aller avec un simulateur comme cela a été fait sur le site The Wizard of Odds. J’ai ainsi programmé un simulateur qui a réalisé 4 milliards de mains à une table où 10 joueurs ne couchaient jamais leurs cartes. Dans les faits, il y a souvent moins que 10 joueurs à la table et il est probable que certains joueurs couchent quelques mains potentiellement gagnantes. Dans ce cas, le simulateur identifie la probabilité maximale. En réalité, la probabilité est moindre.

Le tableau suivant indique la fréquence, en 4 milliards de mains, de chaque combinaison qui donne lieu à une main crève-coeur. Ici, le carré minimal est 9999. Dans ce tableau, la combinaison 0000 indique un carré de 10 et la combinaison 890VD indique une quinte du huit à la dame. Si on lit la ligne VVVV, à la colonne une chance sur, on constate qu’une main crève-coeur d’un carré de valets ou plus a une chance sur 336.700 de survenir (soit p = ,00000297). Cette probabilité est légèrement supérieure à celle obtenue (type 2) par le site The Wizard of Odds parce qu’un milliard et demi de mains simulées est insuffisant pour estimer les combinaisons affichées en rose pâle dans ce tableau. Quatre milliards de mains est un minimum pour obtenir une solution stable. À noter que si le critère était un carré de 10 ou plus, la probabilité augmenterait à une chance sur 268.276. Pour tester différentes mains minimales, il suffit partitionner ce tableau en conséquence.

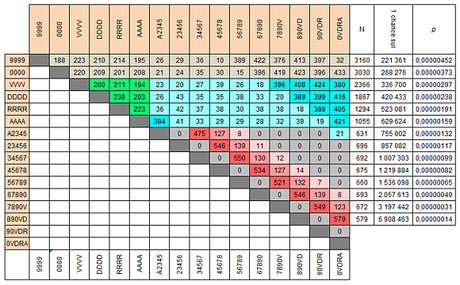
L'estimé empirique est d'une chance sur 1.913.904. C'est très loin de la probabilité maximale d'un chance sur 336.700. Cela est certainement dû au fait qu'il n'y a pas toujours 10 joueurs à table et que certains couchent des mains potentielles. En contrepartie, la probabilité empirique ne tient compte que des mains post-flop. L'écart pourrait aussi être dû à un défaut du mécanisme de tirage des cartes. À vrai dire, on ne sait pas parce qu'on n'a pas les moyens de le vérifier.

C’est intéressant d’estimer la probabilité globale. Mais, c’est aussi intéressant de jeter un coup d’oeil à la probabilité de chacune des combinaisons possible.

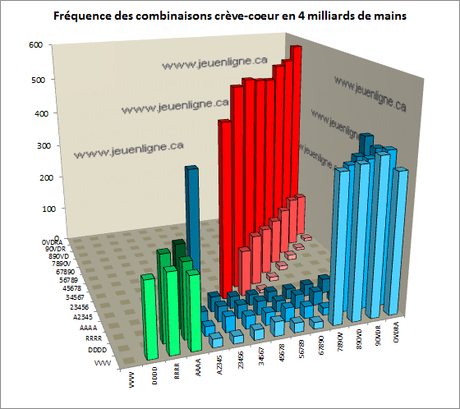
À gauche, en vert, ce sont les combinaisons carré contre carré. En principe, les 6 colonnes en vert devraient être exactement de la même hauteur. Ce n’est pas le cas parce que le générateur de nombres pseudos aléatoires que j’ai utilisé (System.Random de vbnet) n’est pas capable de simuler exactement le hasard à ce niveau de complexité malgré qu’il ait réussi un tas de tests de conformité. Une telle disparité est aussi vraisemblable sur les plateformes de poker en ligne.

En rouge et en rose, figurent les confrontations de quinte contre quinte. En rouge, ce sont les combinaisons réalisées avec seulement 7 cartes (2 pour le joueur 1, 2 pour le joueur 2 et 3 sur la table). En rose foncé, ce sont les combinaisons exigeant 8 cartes. On voit comment la probabilité diminue considérablement. En rose clair, ce sont les combinaisons qui exigent 9 cartes. Leur probabilité est infinitésimale. En principe, sauf distorsion du GNPA, les colonnes en rouge devraient être égales.

En bleu, ce sont les confrontations carré contre quinte. Après les quintes de 7 cartes, la combinaison la plus probable de survenir est une quinte contenant la carte du carré qui est en opposition. Sinon, la probabilité est vraiment moindre (les petites colonnes en bleu).

Bref, tous les jeux ne sont pas également probables. Ceci peut influencer combien d’argent on devrait mettre sur une main … quoique, à défaut de remporter la main crève-coeur, toutes ces mains sont exceptionnellement fortes.

Enfin, voici comment varie la probabilité selon la main que possède un joueur, peu importe ce qu’il y a dans les mains des autres joueurs. Bon amusement!

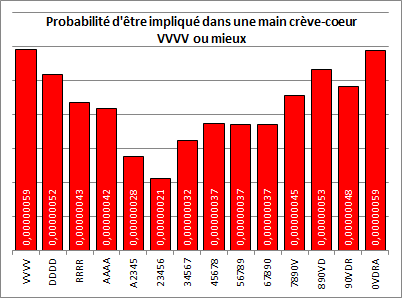
Prochaine étape : Que se passe-t-il s'il n'y a pas 10 joueurs à la table? Ensuite, que se passe-t-il si un joueur en vient à coucher des mains potentielles?
Photo : Nevit