Interfaces, frontières, bords : des archétypes de problèmes transversaux

La médiation technique vise à établir des passerelles entre des secteurs d'activité qui n'ont que peu d'échanges techniques, voire pas du tout. Comme s'il fallait briser un mur invisible.
Or, de manière amusante, on retrouve dans un tas de domaines des problématiques de "murs".

Ubiquité des interfaces

Entendons-nous : je parle de "murs" au sens large. Il peut s'agir :

• d'interfaces entre deux fluides, comme l'eau et les hydrocarbures dans l'extraction pétrolière ;
• de joints de grains, en métallurgie ;
• de bords de solides, en mécanique du contact ;
• de membranes, comme dans le cas de l'osmose en biologie ou en chimie ;
• de frontières, entre les hommes stratégie politique ou militaire, mais aussi entre les espèces en écologie ;
• ou encore de jonction, de contact, de liaison...

En gros, dès lors qu'on est en présence de deux objets amenés à se rencontrer sans qu'ils se mélangent, il y a une zone mince particulièrement intéressante entre les deux, car ses propriétés ne sont généralement pas déductibles des propriétés des deux objets qu'elle sépare.
Difficile de faire plus courant, comme situation, non ? Nous sommes donc en présence d'un phénomène transversal, propice à la médiation technique.

Un exemple : les champs de phase

En effet, comme on retrouve des problèmes d'interface dans plusieurs domaines scientifiques ou technique, il faut s'attendre à ce que certains secteurs soient plus en avance que d'autres sur un problème d'interface identique.
J'illustre mon propos par un exemple purement scientifique. Depuis une vingtaine d'années, certains métallurgistes ont développé une méthode de simulation numérique pour décrire la solidification d'un alliage. Il faut savoir que cette situation donne lieu à des phénomènes complexes, comme l'apparition de figures géométriques très esthétiques appelées dendrites, qui ressemblent fortement à des cristaux de glace.
Pour expliquer l'apparition de ces figures, il a été nécessaire de trouver une manière de décrire la physique de ce phénomène par des équations, et qui permette en particulier de décrire la frontière. Pour simplifier, disons que l'alliage est composé de deux domaines (qu'on appelle des phases) A et B de compositions chimiques différentes.
Il y a plusieurs manières de faire, mais celle que les métallurgistes ont exploré, la méthode du champ de phase, décrivant la matière à l'échelle du micron, est d'apparence assez simple. Si un point de l'espace est dans la phase A, la valeur du champ de phase en ce point vaut 0, et si le point de l'espace est dans B, sa valeur vaut 1. Rien de bien sorcier.
Sauf qu'il faut faire évoluer au cours du temps les valeurs de ce champ de phase. Et c'est là que les physiciens ont été audacieux : ils ont considéré que l'interface entre les deux phases n'était pas infiniment mince, mais qu'elle a une certaine épaisseur (très faible), sur laquelle le champ de phase passe progressivement de 0 à 1. Ce qui permet de considérer que le champ de phase est lisse, et qu'on peut faire des calculs différentiels dessus.
C'est de la triche, me direz-vous : dans la réalité l'interface est brutale (ou en tout cas beaucoup plus raide que dans ces modèles). Oui, mais il faut toujours tricher quand on fait de la simulation numérique, et l'important est de pouvoir réduire l'intensité de la triche à volonté.
Et ils sont arrivés à des résultats très intéressants depuis une vingtaine d'années. La méthode marche, et continue de se développer dans la métallurgie. Pour les fans, suivez ce lien.
Mais ce qu'il y a de formidable, c'est que cette méthode a été déclinée dans d'autres domaines que la métallurgie.
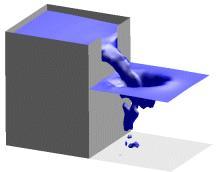
Ainsi, en mécanique des fluides, la méthode VOF est une technique de simulation des liquides à surface libre qui s'inspire fortement de cette technique. À moins que ce ne soit l'inverse, d'ailleurs, car les méthodes ont commencé à être utilisées à la même période, et je serais bien en peine de dire laquelle des deux est la première. Il est même vraisemblable qu'elles se soient fertilisées mutuellement.
Plus tard, une variante du champ de phase, la méthode PFC (Phase Field Crystal) a été développée pour aborder la matière au niveau atomique (donc à une échelle typiquement mille fois inférieure). La matière est discontinue à cette échelle (il y a les atomes et le vide), mais l'idée est de représenter la densité moyennée sur une échelle de temps suffisamment longue à l'échelle de la vibration thermique des atomes.
Par une description mathématique guère plus complexe que sa méthode mère, la méthode PFC arrive à reproduire qualitativement un grand nombre de phénomènes  difficiles à décrire de manière efficace avec les méthodes "traditionnelles" de dynamique moléculaire (qui simulent le déplacement des atomes individuellement), comme la cristallisation ou la vitrification.
Les développements spectaculaires de cette méthode lui permettent d'aborder le problème difficile de la fissuration des solides, ou bien encore les changements de phase (solide-liquide, mais aussi solide-solide).
Métallurgie, mécanique des fluides, mécanique des solides : la technique aurait pu s'arrêter là. Mais on peut également citer des applications à la description des colloïdes (colles, gels), des polymères, des cristaux liquides. Le lecteur passionné (et anglophone) pourra lire à profit cet article d'ArXiv. Il y a même des applications à la biologie cellulaire !

De l'intérêt de la veille transversale

Il paraît impressionnant qu'une technique issue d'un secteur très spécifique trouve des applications dans un grand nombre d'autres domaines. Pourtant, c'est de la nature transversale profonde du problème traité que vient la fertilité de la méthode.
Et de fait, elle n'est pas la seule technique de simulation à connaître un tel succès transversal. On pourrait parler de la méthode des éléments finis, issue de la mécanique des solides, et qui s'est taillée une place dans bon nombre de discipline. J'ai même rencontré des méthodes physiquement réalistes de simulation d'écoulements visqueux à surface libre développés dans l'industrie de l'animation et initialement ignorée dans l'industrie verrière (avant mon intervention) où elle s'est révélée intéressante.
Ce qu'il est important de retenir, c'est qu'un problème technique donné, issu d'un cadre très spécifique à une industrie ou à une discipline, peut souvent être replacé dans un contexte plus large, plus multidisciplinaire. Comment ? Par abstraction des détails spécifiques.
Et c'est le métier du médiateur technique que de permettre cette abstraction.