Mathématiques japonaises

On dit parfois en lisant un texte mathématique : "pour moi c'est du chinois !". Dans ce billet ce sera plutôt du japonais.

Dans son livre "les mathématiques japonaises à l'époque d'Edo" (Vrin, mai 2000), Annick Horiuchi retrace l'histoire du wasan (c'est ainsi qu'on nomme les mathématiques japonaises traditionnelles) de 1600 à 1868. Cette période constitue une sorte de renaissance des mathématiques pour le Japon. Le wasan a donné lieu à une production foisonnante qui s'est inspirée de textes anciens et a su rester indépendante des mathématiques occidentales. Cet essor a été stoppé en 1872 par le nouveau gouvernement de Meiji qui a rendu obligatoire l'enseignement des mathématiques occidentales dans les écoles primaires. 

Le livre montre comment les mathématiciens japonais ont élaboré, à partir d'un manuel du XIIIème siècle, un système original de notations et de techniques de calcul. On peut en avoir un aperçu sur Google Livres ou/et le commander chez amazon.

On trouve, page 82, un problème de géométrie intéressant, que voici :

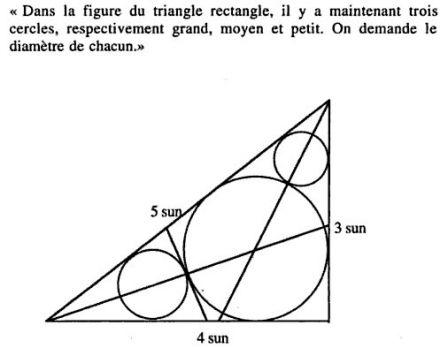
La figure apporte les informations suivantes :

• les dimensions du rectangle sont 3, 4 et 5 sun
• le grand cercle est le cercle inscrit dans le triangle
• les deux autres cercles sont tangents au grand cercle et à deux côtés du triangle.