Le théorème de Pythagore

C'est sans doute le plus célèbre théorème de géométrie, on lui fait même jouer le rôle de Pont aux ânes de la géométrie. Il termine le livre 1 des éléments d'Euclide, comme si tout ce qui précédait n'était là que pour lui, résultat ultime de la géométrie élémentaire.

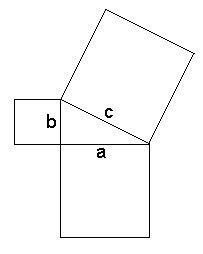
Dans un triangle rectangle,
Le carré de l'hypoténuse,
Est égal, si je ne m'abuse,
A la somme des carrés
Des deux autres côtés.

On trouve  sur curiosphere.tv une vidéo de présentation de Pythagore et de son théorème, dans la série prometteuse des "Petits contes mathématiques". Mais ce que je voudrais mettre en évidence dans ce billet c'est la multiplicité des démonstrations possibles de ce théorème. On annonce parfois une centaine de démonstrations différentes ! Certains ont commencé des recensements, en voici deux exemples :

• le site Cut the knot en présente actuellement 97; le site est rédigé en anglais, mais les démonstrations sont en général très visuelles et se résument souvent à l'exploitation d'une figue.
• le livre "Curiosités géométriques" d’Émile Fourrey (1907) consacre son chapitre 2 au théorème de Pythagore et à la présentation de différentes démonstrations classées en trois types : démonstrations basées sur l'équivalence des figures, démonstrations par transposition d'éléments, démonstrations algébriques. On peut lire le livre sur internet dans la bibliothèque Scientifica du site de la Cité des sciences, on peut aussi en trouver une version papier chez amazon ...

Et encore un troisième exemple qui est la véritable raison d'être de ce billet. J'ai déjà présenté dans le billet Mathématiques sans mots une série d'animations du parti des mathématiques des pingouins. Et bien les pingouins se sont attaqués aux démonstrations du théorème de Pythagore dans une série intitulée 100Way Pythagoras. Il y a déjà 6 démonstrations proposées, voici celle qui doit être d'Euclide.

Je trouve toujours ces animations extraordinaires...