Le problème se pose simplement et ne nécessite que des accessoires élémentaires:
Un carré de papier
Une paire de ciseaux
Un crayon
Une règle
Un compas
La question est de savoir si à l'aide de ces seuls instruments, il est possible de découper un carré en portions... permettant, en les recomposant, de former 3 carrés de plus petites dimensions.
En remplaçant le 3 par un 4 ou un 2, des réponses au problème posé sont quasi immédiates:

Pour recomposer un carré en 2 carrés, il suffit de faire apparaitre le carré central en reliant les milieux de ses cotés, et les quatre triangles rectangles externes se réorganisent en un second carré de mêmes dimensions.
Le problème de la trisection est nettement plus ardu mais pas impossible, contrairement à celui de la quadrature du cercle, par exemple.
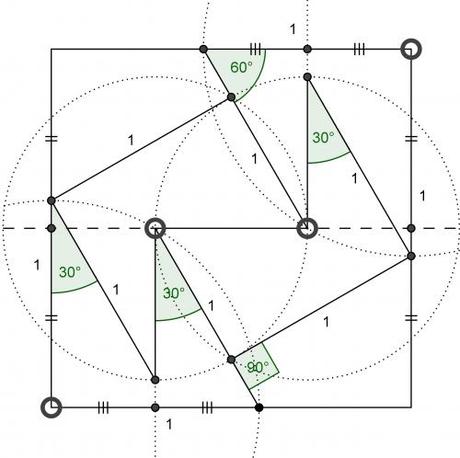
Le problème a été traité par Abu'l Wafa (940,998) pour répondre aux besoins du zellige. Les artisans de l'époque utilisaient des techniques de découpe. Celles-ci étaient très efficaces mais pas exactes d'un point de vue mathématique. Abu'l Wafa proposa une solution exacte avec un morcellement du carré initial en 9 morceaux.
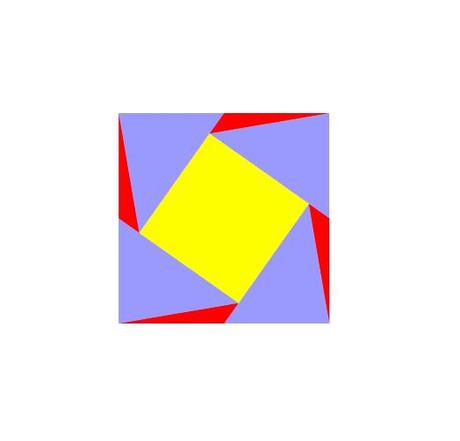
La construction est détaillée dans cet article (lire les commentaires pour la référence du problème inverse et historique).
Cette figure est à mettre en relation avec le motif suivant présent à la mosquée d'Ispahan en Iran:

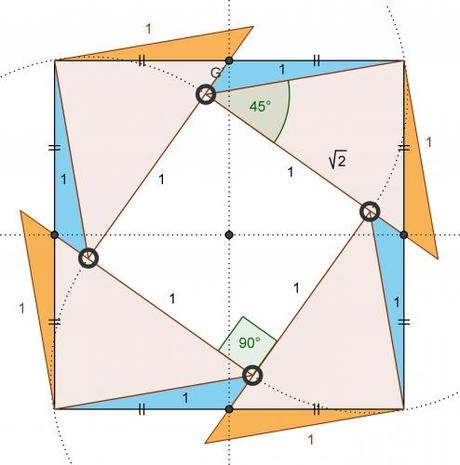
Ce qui est intéressant avec la trisection d'Abu'l Wafa c'est qu'il s'agit d'un cas particulier de découpage de carré que l'on peut généraliser, en apportant en passant une démonstration originale du théorème de Pythagore. C'est ce qu'a montré Henry Perigal. Il a démontré que quelque soit la dimension du carré central, que l'on placera à l'extérieur de l'un des cotés droits du triangle rectangle, il est possible de réaliser le découpage d'un carré dont le coté est l'hypothénuse, en reconstituant le deuxième carré adossé à l'angle droit. Il fut tellement heureux de cette découverte qu'il la fit inscrire sur sa tombe.
Perigal résolut aussi le problème de la trisection du carré comme le montre l'animation suivante à partir du problème inverse: Comment former un carré à partir de trois carrés identiques?
minimisation du nombre de pièces pièces de même aire généralisation de la technique C'est le résultat auquel est parvenu Christian Blanvillain aidé de Janos Pach. Leur solution comporte 6 pièces de même aire et donne une infinité d'autres possibilités par glissement. Le début du raisonnement de C. Blanvillain et J. Pach démarre sur une solution fausse utilisée par les artisans avant Abu'l Wafa.
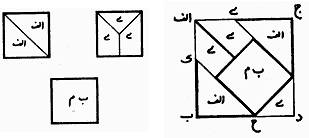
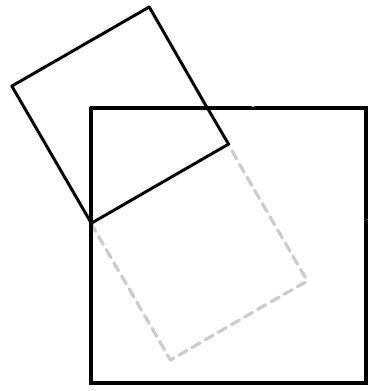
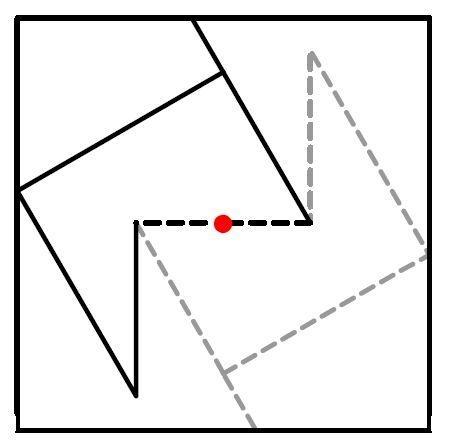
La recomposition des 3 carrés se fait de la façon suivante:
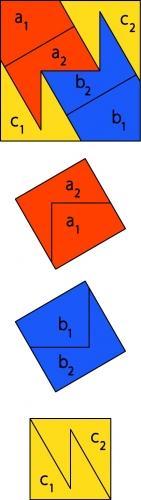
L'historique de la trisection du carré et les explications de celle de Christian Blanvillain sont détaillées dans un article qu'il a déposé sur Arxiv.
Images sauf gif animé: C. Blanvillain
Animation gif: O. Leguay et fichier original ICI
