Je ne connaissais pas ce théorème mais il est génial et utilisable par les plus petits.
Il suffit de prendre une feuille de papier pointé et d'y tracer un polygone aux sommets de coordonnées entières, comme dans l'exemple suivant :
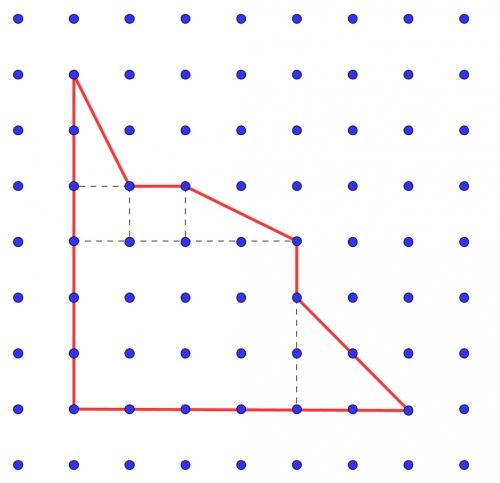
* On peut facilement calculer son aire de façon additive à l'aide des pointillés.
Ce polygone est constitué d'un grand rectangle d'aire 12 et de deux petits carrés d'aire 1 soit 12+1+1=14.
Il est aussi constiué de 3 triangles d'aire la moitié des aires des rectangles (ou carrés) associés soit: 2+1+1=4.
L'aire de ce polygone est donc de 14+4=18.
* Utilisons maintenant le théorème de Pick:
Déterminons le nombre de points intérieurs à ce polygone : 10
Calculons la moitié du nombre de points du contour : 18/2=9
Enlevons 1
10+9-1=18
Surprenant et simple non ?
Jeu de briques
Snake
Pacman
Bubble