Valeur acquise par une suite d'annuités constantes ou la puissance des intérêts composés !

Après avoir découvert plusieurs sites sur le thème de la richesse et de l'indépendance financière, j'ai eu l'idée d'apporter quelques éléments d'ordre mathématique sur ces fameux intérêts composés...
Vous allez ainsi découvrir les avantages à long terme de l'épargne régulière ou comment devenir riche en laissant faire le temps ;)
Epargner rapporte beaucoup et placer de l'argent sans y toucher, par exemple sur des OPCVM, s'avère très judicieux dès le commencement d'une vie active.
Tout d'abord voici la formule permettant de calculer la valeur acquise par une suite d'annuités constantes, ou plus simplement pour les non matheux le capital obtenu au bout d'un certain temps, en épargnant régulièrement une somme d'argent, le tout placé à un certain taux.

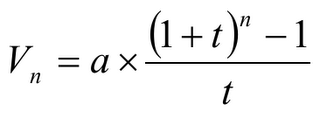
- n correspond au nombre de périodes de placement ; cela peut être un nombre de mois, d'années, de trimestres, de quinzaines... etc
on parle alors de capitalisation mensuelle, annuelle... (les intérêts sont rajoutés au capital tous les mois, tous les ans...)
Pour la plupart des personnes cette période est souvent le mois étant donné que l'on peut mettre de côté son argent tous les mois après avoir reçu son salaire.
- t correspond au taux de placement (connu d'avance ou espéré)
ce taux peut être un taux périodique proportionnel (taux annuel ramené au taux mensuel en divisant par 12) ou un taux périodique équivalent.
pour le taux équivalent il faut considérer ceci :

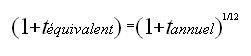
- a correspond à l'annuité c'est à dire la somme placée régulièrement, ici une somme constante (tous les mois par exemple)
- Vn correspond au capital au bout de n périodes (au bout de 25 ans par exemple)
Pour les personnes qui ont quelques connaissances en mathématiques, d'où vient cette formule ?
c'est assez simple en fait !
il faut utiliser la formule donnant la valeur acquise par un capital placé à intérêts composés :

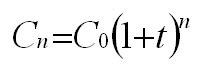
ensuite, chaque somme placée régulièrement est un terme d'une suite géométrique de raison (1+t)... le dernier versement produit des intérêts pendant 1 mois, l'avant dernier pendant 2 mois... etc et le premier versement pendant n mois.
le Vn de notre formule de départ est donc la somme des termes d'une suite géométrique de premier terme a et de raison (1+t).
je ne détaillerai pas ici la formule de la somme des termes d'une suite géométrique, à vous de travailler !
Après toutes ces explications ennuyeuses, et pour celles et ceux qui n'ont pas déjà cliqué ailleurs, je vous propose un petit fichier Excel pour utiliser concrètement cette formule.
télécharger le fichier Excel
J'ai utilisé le taux périodique équivalent pour la lettre t de la formule.
J'ai réalisé moi-même ce fichier, donc n'hésitez pas à le modifier à votre guise ou à me signaler des erreurs.
Bonne simulation !
Sylvain