Mesurer la diversité: oui mais comment ?

Depuis une vingtaine d'années, un important problème rencontré dans la conservation des espèces est la mesure de la diversité. Cette notion intervient pour savoir quelles espèces en priorité doivent être protégées. La possibilité d'une mesure de la diversité peut d'ailleurs s'étendre à de nombreux autres domaines.

Le sujet contient en fait deux difficultés, la première est d'évaluer la diversité de deux éléments et de la convertir en une quantité que l'on pourrait assimiler à une distance, la seconde est d'évaluer la diversité d'un groupe en utilisant les "distances" deux à deux précédentes et de pouvoir la comparer à celle d'un autre groupe. C'est ce deuxième point que nous allons aborder ici et tenter d'établir s'il peut exister une définition axiomatique de la diversité, au sens de la comparaison de deux ensembles comportant le même nombre d'individus.

Avant d'aller plus loin, il peut être important de définir ce que les matheux appellent une axiomatique. Les mathématiques reposent sur le raisonnement logico-déductif. Des propositions vraies se déduisent des propositions vraies, mais si l'on remonte à l'envers, on trouve une origine, on aperçoit ce qui est primitif, les bases sur lesquelles s'appuient le raisonnement. Par exemple, la géométrie plane s'appuie sur quelques axiomes que l'on trouve dans les Eléments d'Euclide. La difficulté principale des mathématiciens ayant été de déterminer combien d'axiomes il fallait au minimum pour pouvoir construire toute la géométrie. Ils hésitèrent très longtemps entre 4 et 5, voulant faire la démonstration de la 5ème proposition, ce qui s'est avéré impossible puisqu'il s'agissait d'un axiome. Le changer revenait à changer de géométrie. Les contraintes sur les axiomes sont très fortes: d'une part il ne doit pas en manquer puisque ce sont sur eux que reposeront toutes les mathématiques, il ne doit pas non plus y en avoir plus que le strict nécessaire et d'autre part, ils ne doivent pas introduire de contradiction. 

Si l'on veut établir quels sont les axiomes qui permettront une mesure pertinente de la diversité, ceux-ci devront être en nombre minimal et deux ensembles de diversité distinctes devront avoir des mesures classées dans le même ordre que celui de leur diversité.

Regardons d'un peu plus près comment le problème se pose, par exemple en partant d'un arbre phylogénétique, dont on a converti l'éloignement des individus (noeuds) en distances:

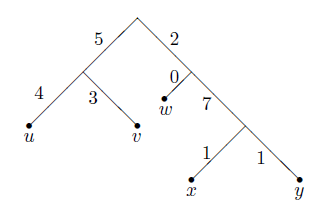
Considérons par exemple les ensembles {u,x,y} et {u,w,y}. Le premier est moins diversifié que le second, compte tenu du fait qu'aucun membre du second ensemble n'est proche d'un autre alors que x et y le sont dans le premier. Cependant si l'on mesure la "distance" totale entre les 3 éléments on obtient 20 pour le premier et 19 pour le second, ce qui n'est pas compatible avec une mesure de la diversité.

L'objectif de ce billet est de ne pas utiliser de formalisme mathématique afin de rendre le sujet le plus accessible possible. Ce travail est issu du questionnement de Chris Dowden de l'École Polytechnique, qui s'est intérrogé d'une part sur la construction des axiomes, et aussi de l'absence d'une telle réflexion en mathématiques. On pourra donc consulter le document original ICI.

Les quatre premiers axiomes:

1) Si l'on rajoute un élément distinct à un ensemble, la mesure de la diversité de ce nouvel ensemble  est supérieure à celle de l'ensemble initial et il y a égalité si l'élément est déjà dans l'ensemble.

2) Soient deux ensembles ayant le même nombre d'éléments. Si les distances  des éléments pris deux à deux du premier ensemble sont supérieures aux distances des éléments pris deux à deux du second ensemble, la mesure de la diversité du premier ensemble est supérieure à celle du seconde et il y a égalité si toutes les distances deux à deux sont égales de part et d'autre.

3) Axiome de continuité.
Soit un ensemble S et une mesure de diversité quelconque d (entre deux ensembles et aussi petite que l'on veut), il existe un écart e tel que pour tout ensemble T tel que l'écart entre les distances de tous  les éléments pris deux à deux, une paire dans S et une autre dans T  soit inférieure à e, on peut rendre la mesure  de la diversité entre les deux ensembles inférieure à d.

Note: les matheux y verront l'analogie avec la notion de continuité dans les réels.

4) Axiome de l'invariance d'échelle
Soient 4 ensembles.  A et A' ont même nombre d'éléments et B et B' aussi. S'il existe un coefficient multiplicateur entre les distances de tous les élements pris deux à deux, une paire dans A et A' identique à celui existant entre les paires de B et de B'. Si la diversité de A est supérieure à celle de B, il en est de même pour A' et B' et réciproquement.

Trouver une bonne candidate pour la mesure de la diversité...

Il  est tout à fait possible de construire une mesure de la diversité satisfaisant ces quatre premiers axiomes. Il y a existence mais pas unicité. Cette mesure est associée à une fonction qui convient, le travail étant de construire "proprement" cette fonction afin qu'elle satisfasse aux axiomes-contraintes et que tous soient satisfaits quelque soient les situations rencontrées. Et c'est là que le bât blesse, et sans doute manque-t-il un axiome contrainte pour qu'il n'y ait pas de résultat contre intuitif sur un cas particulier. Prenons par exemple la situation suivante:

L'ensemble S est moins diversifié que l'ensemble S' car le noeud S4 est plus proche des trois autres que le noeud s'4 alors que les trois noeuds s1, s2 et s3 sont dans la même configuration dans les deux ensembles, chacun éloignés d'une unité.

Un axiome doit donc être ajouté aux précédents afin que la mesure de diversité choisie soit capable de classer les ensembles S et S' correctement, ce qui n'est pas le cas pour les premières mesures trouvées satisfaisant seulement les quatre premiers axiomes.

Le cinquième axiome

Cet axiome aborde la question de la diversité d'un ensemble à 3 éléments et indique que tous les ensembles à 3 éléments qui possèdent un "éloignement total" identique (ici 1+1+1=1+1/3+4/3) sont tels que ceux dont la somme des écarts au tiers de cette valeur ici 3/3=1 est la plus grande , sont aussi  les moins diversifiés. Par exemple, dans le cas présent les triplets (1,1,1) sont moins plus diversifiés que le triplet (1/3,4/3,1). Dans le premier ensemble la somme des écarts à 1 est nulle alors que ce n'est pas le cas pour le second.

Et pendant qu'on y est, généralisons...

Il faudrait en fait généraliser ce cinquième axiome aux sous-ensembles de toutes dimensions inclus dans deux ensembles contenant le même nombre d'éléments dont on souhaiterait comparer la diversité. On ne risquerait plus de "manquer" un écart caché.

Oui mais...

Ce cinquième axiome, tel qu'il est formulé, est incompatible avec les premiers axiomes! Il rend inconsistant les mathématiques que l'on peut faire avec ces seules règles. Avec ces règles nous pourrions démontrer un résultat et son contraire.  Et zut. On y était presque.

Alors remettons l'ouvrage sur le métier

Il est possible de concevoir une formulation du cinquième axiome qui semble compatible avec les quatre premiers exemples. Les premiers exemples sont prometteurs en attendant une démonstration, ce qui laisse envisager une ouverture vers ce domaine des mathématiques encore presque vierge: celui de l'évaluation de la diversité de deux ensembles ayant même nombre d'éléments.