Algorithmique : optimiser le nombre de transactions

Ca fait aujourd'hui un certain bout de temps que je n'ai plus mis à jour ce blog. C'est l'occasion donc de vous partager ce petit script qui m'a occupé pendant un dimanche après-midi d'hiver quand je m'embêtais ... Je m'étais pris la tête sur un problème la veille au soir, et je m'étais juré d'essayer de trouver une solution la plus optimale possible pour le régler.

Je vais donc essayer de vous expliquer le problème de la manière la plus simple qui soit. C'est d'ailleurs un problème que vous avez surement déjà rencontré dans votre vie de tous les jours. C'est hyper basique, mais on ne se rend pas toujours compte qu'il cache quand même un peu de subtilité (comme quoi, quand on est geek on peut s'occuper avec très peu )

Lorsque vous êtes en vacances avec des amis et que vous demandez à chacun de tenir ses comptes, vient la fin des vacances où il faut évidement équilibrer les comptes. Alors tant qu'on n'est pas parti à plus de 4 en vacances c'est en général encore le genre de calculs abordables à conditions que les comptes ont bien été tenus, mais lorsque le nombre de participants augmente, la complexité du problème augmente de manière exponentielle pour notre petit cerveau. En effet, notre bon sens voudrait optimiser le nombre de remboursements pour se "faciliter" la vie, mais on se rend vite compte que cette optimisation est compliquée.

C'est l'autre jour en passant la soirée à bouffer des brochettes et à boire quelques bieres autour d'un feu de camp avant une nuit à la belle étoile qu'on a discuté de ce problème avec un ami qui est le fondateur de tricount (que vous connaissez surement, et si vous ne connaissez pas, utilisez le, c'est vraiment bien) Il semblait me dire que le problème est difficilement scalable lorsque le nombre de participants augmente de manière drastique.

Prennons un exemple pour illustrer le problème : Nous sommes partis en vacances à 4 et à la fin des vacances nous obtenons le résultat suivant :

• Tom a dépensé 10 EUR
• Bob a dépensé 100 EUR
• Guy a dépensé 70 EUR
• Val a dépensé 20 EUR

En total, on a dépensé 200 EUR. Donc chacun aurait du dépenser 50 EUR. Pour ré-équilibrer exprimons ça sous forme de compte (ceux qui sont en négatif doivent de l'argent, ceux qui sont en positif doivent recevoir de l'argent) :

• Tom : -40 EUR
• Bob : 50 EUR
• Guy : 20 EUR
• Val : -30 EUR

On voit désormais clairement que pour optimiser le nombre de transactions pour le remboursement, il faut chipoter un peu, et plusieurs solutions sont possibles : Solution 1 :

• Tom rembourse 40 EUR à Bob
• Val rembourse 20 EUR à Guy
• Val rembourse 10 EUR à Bob

Solution 2 :

• Tom rembourse 20 EUR à Guy
• Tom rembourse 20 EUR à Bob
• Val rembourse 30 EUR à Bob

Dans ce cas ci les 2 solutions proposent un nombre de transactions similaires. Mais ça n'est pas toujours le cas. De plus, si on voulait optimiser ce choix, qu'est-ce qui nous ferais choisir pour la solution 1 ou la solution 2?

Et si le nombre de participants était de X ... est-ce que le problème ne serait pas encore plus complexe?

J'ai donc essayé d'écrire un petit algorithme qui propose une solution. Qu'on pourrait peut-être améliorer. Je vous invite à vous pencher sur la question aussi :

Tant que tous les comptes ne sont pas à 0 :
    X = celui qui doit le plus d'argent
    Y = celui a qui on doit le plus d'argent
    X rembourse un maximum a Y

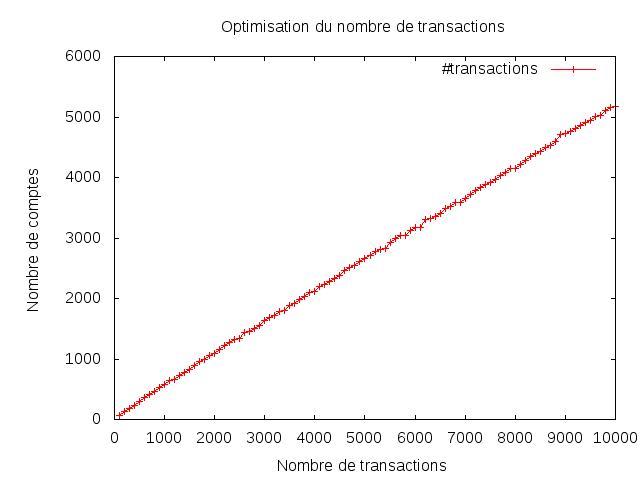
Je suis sur que cet algorithme peut encore être amélioré ! En ce moment j'ai des performances en O(n) au niveau de mon petit script python que vous pourrez lire ci-dessous. Je suis toujours intéressé par les solutions plus optimales (après tout, je n'ai que passé quelques heures sur le problème)

Vous pouvez télécharger le script python ici : algo.py