LHC : Objectif 2010 atteint

LHC : Objectif 2010 atteint

La semaine dernière, le CERN annonçait fièrement que le LHC avait atteint ses objectifs pour 2010 : la machine a délivré 2 inverse picobarns aux différents détecteurs, or, la plupart des gens n’ont jamais entendu le mot « picobarn » de leur vie… La raison est simple: peu de gens sont physiciens des particules !

Collision proton-proton dans le détecteur CMS du LHC le 9 Juillet 2010. © CERN.

Je n’appartiens pas non plus à la catégorie des physiciens des particules, néanmoins j’entends souvent ces mots au CERN lors de communiqués officiels comme celui-ci.  J’ai donc cherché à savoir ce que se cachait derrière ces mots abscons pour nous autres, les personnes « normales ».

Le Barn

Le barn est tout simplement une unité de surface étant de l’ordre de la section géométrique du noyau d’un atome. En gros, vous prenez le noyau d’un atome (ayant un rayon d’environ 10^-12 cm), vous le coupez en deux et la surface de cette coupe est environ égale à 1 barn, soit 0,00000000000000000000001cm², ou plus simplement 10^-24 cm². Par exemple, le noyau d’un atome d’uranium (un des plus gros noyaux) possède une section géométrique de 1,5 barn.

Section efficace et géométrique

Le problème c’est que lorsqu’on observe des réactions nucléaires (interactions entre les noyaux des atomes), ou des collisions de particules entres elles ou contre des cibles, les atomes paraissent avoir une section plus grande ou plus faible selon les phénomènes observés. Pour rendre compte de ce problème, les physiciens ont alors introduit une section dite efficace, plus significative que la section géométrique réelle des noyaux des atomes. La section efficace d’un noyau, représentée par la lettre grecque sigma, n’est pas constante pour une particule donnée et est finalement assez peu dépendante de la taille réelle du noyau mais varie significativement selon sa vitesse et le type de réaction ou collision.

Cette section efficace rend compte de la probabilité d’interaction d’une particule pour une réaction précise (une collision, une réaction nucléaire, etc). Plus la section efficace est élevée, plus la réaction étudiée a des chances de se réaliser. Par exemple, la section efficace de l’absorption d’un neutron lent dans la matière est supérieure à 1000 barns alors que la section efficace des phénomènes étudiés dans les collisions des accélérateurs de particules comme le LHC est de l’ordre du picobarn (10^-12 barn), voir du femtobarn (10^-15 barn).  Un femtobarn, c’est comme si les noyaux était un million de milliards de fois plus petit (et dieu sait s’ils sont déjà petit).

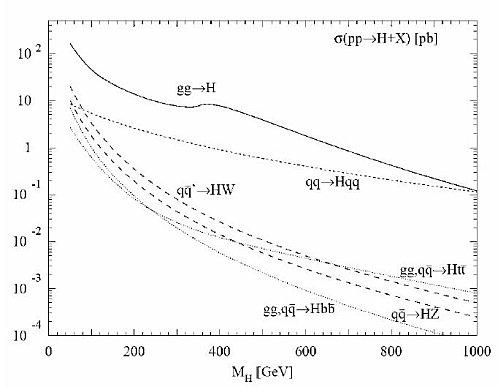
Autant dire que les accélérateurs recherchent des évènements extrêmement rares à observer dans une collision. Prenons le cas du LHC et du fameux boson de Higgs tant recherché. Nous ne connaissons pas encore sa masse exacte, si elle existe, mais on peut toutefois calculer la section efficace de différents phénomènes pouvant lui donner naissance dans le LHC. La figure ci-dessous nous dit que la section efficace du boson de Higgs pourrait se situer entre 10 picobarns et 0,1 femtobarn selon les différents phénomènes possibles si sa masse est comprise entre 300 GeV et 1000 GeV. Autrement dit: Il faut enregistrer au moins dix milles milliards de collisions pour avoir la chance de voir un Higgs !!!

Sections efficaces possibles pour la production d’un boson de Higgs dans le LHC en fonction de la masse de ce dernier. Dan Green, Fermilab (2005)

La luminosité

On aura donc compris la chose suivante: ce qui intéresse les accélérateurs de particules, c’est de produire le plus de collisions possibles.

Pour évaluer cette capacité, on calcule une grandeur appelée luminosité. Le principe en est simple : compter le nombre de particules qui se croisent dans un cm² à chaque seconde. Ainsi, la luminosité est calculée par la formule suivante :

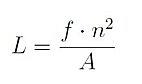
avec f la fréquence de croisement des paquets de particules, n le nombre de particules par paquet et A la section géométrique du faisceau de particules. Dans le cas du LHC, au point nominal, on obtient :

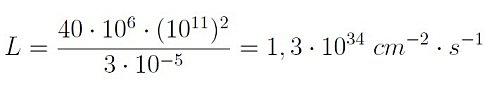
Ce grand chiffre signifie que dix millions de milliards de milliards de milliards de particules se croisent dans un centimètre carré toute les secondes dans le LHC…

Luminosité intégrée

Le paramètre intéressant à calculer par la suite est naturellement la luminosité intégrée qui correspond à la luminosité accumulée dans le temps (c’est-à-dire la luminosité multiplier par le temps de collision de la machine). Si on reprend le cas du LHC au point de fonctionnement maximum, en 90 secondes, la machine peut ainsi fournir une luminosité intégrée de 1,3*10³⁴ * 90 = 10³⁶ cm^-2. Pour plus de facilité, on convertit ce chiffre en barn inverse (1 b^-1 = 10²⁴ cm^-2), on obtient alors une luminosité intégrée de 10¹² b^-1 = 1 pb^-1, soit un inverse picobarn pour 90 secondes de collision dans le LHC.

Le 10 août dernier, un détecteur de particules du LHC, ATLAS, annonçait avoir franchis la barre de 1 inverse picobarn. © ATLAS.

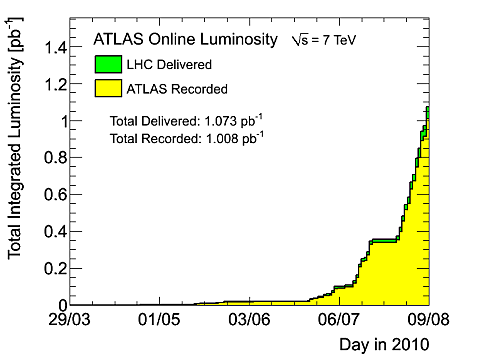
Etat des lieux du LHC

En ce mois d’octobre, le LHC a accumulé 2 inverse picobarns depuis sa mise en route fin mars 2010 car la machine ne fonctionne pas encore à sa luminosité maximale. Cependant, cette machine fonctionne de mieux en mieux : entre mars et août, le LHC avait fournit environ 1 inverse picobarn alors que  la semaine dernière, il lui a fallu seulement 13h pour fournir un autre inverse picobarn (la luminosité maximale était de 10³², soit 100 inverse microbarns par seconde). A titre de comparaison, il a fallu 2 ans au Tevatron  pour atteindre cette luminosité (l’autre grand accélérateur de particules aux Etats-Unis).

L’objectif du LHC pour 2010 a ainsi été accompli en ce mois d’octobre (2 inverse picobarns). Pour 2011, la machine doit atteindre un total de 1 inverse femtobarn, soit 500 fois plus. Il ne faut pas oublier que la plupart des particules recherchées par les détecteurs du LHC sont  produites par des collisions ayant une section efficace entre 1 picobarn et 1 femtobarn, il faudra donc attendre que cette quantité de données soit dépassée pour pouvoir annoncer des résultats sérieux. A suivre en 2011...

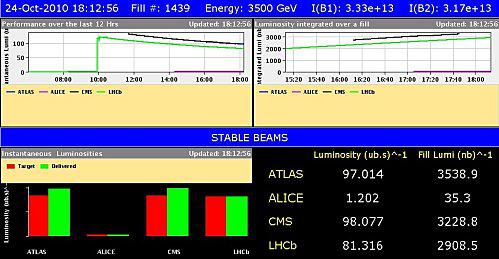
Etat du LHC en ce dimanche 24 octobre au soir : les détecteurs ont une luminosité d'environ 100 inverse microbarn par seconde chacun.

Par Benjamin Bradu - Publié dans : Phys. Particules/Quantique
Ecrire un commentaire 0 - Voir le commentaire - Voir les 0 commentaires - Partager   ' ); YAHOO.util.Selector.query( 'input', dial.getEl(), true ).focus(); }, this, true ); return false; " title="Partager par adresse simplifiée">     Précédent : Charpak et sa chambre à fils Retour à l'accueil