La page du dimanche 27 juin 2010

Idiomathique du jour

On peut demander l'addition à un garçon de café sans pour autant le prendre pour une bête de somme.

Max Dehn et le 3ème problème de Hilbert

Le mathématicien allemand Max Dehn est mort le 27 juin 1952.
En 1900, il a aussi résolu le troisième problème de Hilbert.
En dimension 2, lorsque 2 polygones ont même aire, il est toujours possible de découper l'un en polygones qui permettent de former le second; c'est le théorème de Wallace-Bolyai-Gerwein. Le 3ème problème de Hilbert pose la question pour la dimension 3 : étant donnés deux polyèdres d'égal volume, est-il possible de découper le premier polyèdre en des polyèdres qu'on peut rassembler pour former le second ?
Max Dehn a démontré que ce n'était pas toujours possible. Pour ce faire, il a introduit une grandeur, maintenant appelée invariant de Dehn, qui devait être la même pour deux polyèdres lorsque le passage de l'un à l'autre par découpage était possible. Il a alors pu conclure en montrant qu'un cube et un tétraèdre régulier n'avaient pas le même invariant de Dehn.
Citation :
Les mathématiques sont la seule matière qui peut être enseignée sans aucun dogmatisme.

Sophie Germain

La mathématicienne française Marie-Sophie Germain est morte le 27 juin 1831.
En arithmétique, elle nous a laissé le théorème de Sophie Germain (pour tout entier naturel n strictement plus grand que 1, n^4 + 4 n'est pas premier) et les nombres premiers de Sophie Germain.
Elle est aussi connue pour ses échanges avec le mathématicien Carl Friedrich Gauss et pour ses travaux sur l'élasticité des corps.

Auguste De Morgan

Le mathématicien britannique Auguste De Morgan est né le 27 juin 1806.
Fondateur avec Boole de la logique moderne, il a notamment formulé les lois de De Morgan:
- La négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions, ce qui signifie non(A et B) est (non A) ou (non B).
- La négation de la disjonction de deux propositions est équivalente à la conjonction des négations des deux propositions, ce qui signifie que non(A ou B) est (non A) et (non B).
ou pour être plus concis et peut être plus clair :


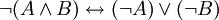
Citations :

- Le moteur de l'invention mathématique n'est pas le raisonnement 
mais l'imagination.
- Quand on lui demandait son âge, il répondait : 
j'avais x ans en l'an x².
- Imaginez une personne qui n'a pas peur du ridicule. Elle
pourrait vous dire : premièrement, un nombre négatif n'a pas
de logarithme; deuxièmement, un nombre négatif n'a pas de racine
carrée; troisièmement, le rapport entre ces deux nombres qui
n'existent pas est égal au rapport entre la circonférence et le
diamètre d'un cercle.