Nombres Univers

Pi est un nombre irrationel (il est même “ "transcendant“ ") : comme il ne peut pas s’écrire sous forme d’une fraction, ses décimales ne “ "cyclent” " jamais commes celles de 22/7 = 3.142857 142857 142857 … par exemple, et il y en a une infinité, donc a priori une infinité de séquences de décimales toutes différentes.

Pas étonnant donc qu’on puisse facilement trouver sa date de naissance dans les décimales de Pi, mais est-on sur de trouver n’importe quelle séquence (finie) de chiffres dans les décimales de Pi, par exemple un million de chiffres 5 consécutifs, ou l’oeuvre complète de Shakespeare traduite en chiffres ? Pour ça, il faudrait que pi soit un “ "nombre univers“ ". Et n’en déplaise à certains, on n’en sait rien pour l’instant*, et il en va de même pour e,

, ln(2) et tous les nombres irrationnels usuels, et ce non seulement en base 10 mais dans n’importe quelle base [1].

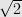
Par contre il existe une infinité de nombres univers, on sait les fabriquer, et c’est même très facile. Exemple: la constante_de_Champernowne. On la forme en concaténant simplement les entiers croissants dans les décimales :

C₁₀=0,123456789101112131415161718192021…

Les nombres ainsi construits sont même plus qu’univers, ce sont des nombres “ "normaux” " parce que toute séquence de décimales finie se répète indéfiniment avec une probabilité uniforme. Dans C10, la séquence 1234 du début va se trouver plus loin …1233 1234 1235… et encore plus loin  …11233 11234 11235… et ainsi de suite jusqu’à l’infini. La séquence 1234 se retrouve statistiquement dans 1/10000 ème des groupes de 4 décimales.

Un nombre univers compact ?

Les nombres normaux font un beau gâchis de décimales, car ils contiennent l’oeuvre complète de Shakespeare une infinité de fois. Peut-on imaginer un nombre univers plus économique ?

Essayons de compacter la constante_de_Champernowne en:

1. ne répétant pas les décimales déjà présentes. Par exemple après 0,1234567891011 , on ne va pas écrire 12 parce que le 1 est déjà présent, mais seulement 2 : 0,12345678910112 …
2. ne répétant pas les nombres déjà présents dans les décimales précédentes : dans l’exemple ci-dessus, le 12 est déjà présent dans les toutes premières décimales, donc on peut passer directement au 13 :

on obtient ainsi 0,123456789 10113141516171819 20212242526272829 3032335 …

On voit qu’on ne gagne que quelques pourcents de décimales. Mais on peut aller plus loin : les 9 premières décimales de C10 ne servent à rien puisqu’elles sont forcément présentes dans les décimales de 10..à..99, lesquelles ne servent à rien puisqu’elles figurent 10x dans les décimales de 100..à..999 et ainsi de suite.

Ses séquences de De Bruijn

Une tresse de De Bruijn

Mais d’abord, est-ce bien malin de fabriquer un nombre univers compact en concaténant des entiers consécutifs ? Peut-on fabriquer une séquence contenant chaque nombre de n décimales et qui soit nettement plus compacte que l’énumération ? Jean-Paul Alllouche m’a gentiment indiqué que les séquences De Brujin (SDB) font exactement ça, et même très bien puisque chaque nombre de n chiffres en base b n’est présent qu’une seule fois dans la séquence B(b,n). La page Wikipédia sur les SDB (en anglais) pointe sur un site étonnant : le “ "Combinatorial Object Server” " qui comporte entre autres outils un générateur de SDB permettant de générer très rapidement par exemple :

B(10,3) = 0 0 0 1 0 0 2 0 0 3 0 0 4 0 0 5 0 0 6 0 0 7 0 0 8 0 0 9 0 1 1 0 1 2 0 1 3 0 1 4 0 1 5 0 1 6 0 1 7 0 1 8 0 1 9 0 2 1 0 2 2 0 2 3 0 2 4 0 2 5 0 2 6 0 2 7 0 2 8 0 2 9 0 3 1 0 3 2 0 3 3 0 3 4 0 3 5 0 3 6 0 3 7 0 3 8 0 3 9 0 4 1 0 4 2 0 4 3 0 4 4 0 4 5 0 4 6 0 4 7 0 4 8 0 4 9 0 5 1 0 5 2 0 5 3 0 5 4 0 5 5 0 5 6 0 5 7 0 5 8 0 5 9 0 6 1 0 6 2 0 6 3 0 6 4 0 6 5 0 6 6 0 6 7 0 6 8 0 6 9 0 7 1 0 7 2 0 7 3 0 7 4 0 7 5 0 7 6 0 7 7 0 7 8 0 7 9 0 8 1 0 8 2 0 8 3 0 8 4 0 8 5 0 8 6 0 8 7 0 8 8 0 8 9 0 9 1 0 9 2 0 9 3 0 9 4 0 9 5 0 9 6 0 9 7 0 9 8 0 9 9 1 1 1 2 1 1 3 1 1 4 1 1 5 1 1 6 1 1 7 1 1 8 1 1 9 1 2 2 1 2 3 1 2 4 1 2 5 1 2 6 1 2 7 1 2 8 1 2 9 1 3 2 1 3 3 1 3 4 1 3 5 1 3 6 1 3 7 1 3 8 1 3 9 1 4 2 1 4 3 1 4 4 1 4 5 1 4 6 1 4 7 1 4 8 1 4 9 1 5 2 1 5 3 1 5 4 1 5 5 1 5 6 1 5 7 1 5 8 1 5 9 1 6 2 1 6 3 1 6 4 1 6 5 1 6 6 1 6 7 1 6 8 1 6 9 1 7 2 1 7 3 1 7 4 1 7 5 1 7 6 1 7 7 1 7 8 1 7 9 1 8 2 1 8 3 1 8 4 1 8 5 1 8 6 1 8 7 1 8 8 1 8 9 1 9 2 1 9 3 1 9 4 1 9 5 1 9 6 1 9 7 1 9 8 1 9 9 2 2 2 3 2 2 4 2 2 5 2 2 6 2 2 7 2 2 8 2 2 9 2 3 3 2 3 4 2 3 5 2 3 6 2 3 7 2 3 8 2 3 9 2 4 3 2 4 4 2 4 5 2 4 6 2 4 7 2 4 8 2 4 9 2 5 3 2 5 4 2 5 5 2 5 6 2 5 7 2 5 8 2 5 9 2 6 3 2 6 4 2 6 5 2 6 6 2 6 7 2 6 8 2 6 9 2 7 3 2 7 4 2 7 5 2 7 6 2 7 7 2 7 8 2 7 9 2 8 3 2 8 4 2 8 5 2 8 6 2 8 7 2 8 8 2 8 9 2 9 3 2 9 4 2 9 5 2 9 6 2 9 7 2 9 8 2 9 9 3 3 3 4 3 3 5 3 3 6 3 3 7 3 3 8 3 3 9 3 4 4 3 4 5 3 4 6 3 4 7 3 4 8 3 4 9 3 5 4 3 5 5 3 5 6 3 5 7 3 5 8 3 5 9 3 6 4 3 6 5 3 6 6 3 6 7 3 6 8 3 6 9 3 7 4 3 7 5 3 7 6 3 7 7 3 7 8 3 7 9 3 8 4 3 8 5 3 8 6 3 8 7 3 8 8 3 8 9 3 9 4 3 9 5 3 9 6 3 9 7 3 9 8 3 9 9 4 4 4 5 4 4 6 4 4 7 4 4 8 4 4 9 4 5 5 4 5 6 4 5 7 4 5 8 4 5 9 4 6 5 4 6 6 4 6 7 4 6 8 4 6 9 4 7 5 4 7 6 4 7 7 4 7 8 4 7 9 4 8 5 4 8 6 4 8 7 4 8 8 4 8 9 4 9 5 4 9 6 4 9 7 4 9 8 4 9 9 5 5 5 6 5 5 7 5 5 8 5 5 9 5 6 6 5 6 7 5 6 8 5 6 9 5 7 6 5 7 7 5 7 8 5 7 9 5 8 6 5 8 7 5 8 8 5 8 9 5 9 6 5 9 7 5 9 8 5 9 9 6 6 6 7 6 6 8 6 6 9 6 7 7 6 7 8 6 7 9 6 8 7 6 8 8 6 8 9 6 9 7 6 9 8 6 9 9 7 7 7 8 7 7 9 7 8 8 7 8 9 7 9 8 7 9 9 8 8 8 9 8 9 9 9

qui ne comporte que 1000 chiffres au lieu des 3000 qui seraient nécessaires pour une énumération. Si vous êtes observateur, vous remarquerez que 900 n’est pas présent dans la séquence. C’est parce qu’elle est cyclique, il faut l’imaginer “ "bouclée” " et alors les 00 du début de la séquence dont on pouvait penser qu’ils étaient inutiles se placent après le 9 final pour former le 900.

Cette nature cyclique permet donc  de commencer la séquence B(b,n) n’importe où en prenant n chiffres, puis de passer au suivant en se décalant d’un chiffre soit vers la gauche soit vers la droite et ainsi de suite. Après avoir effectué ainsi bⁿ décalages, on se retrouve au point de départ en ayant la certitude d’être passé une et une seule fois par chaque nombre compris entre 0 et bⁿ-1. Beau, non ?

Et utile. Par exemple pour ouvrir une porte protégée par un code de 3 chiffres sans touche “ "entrée” ", qui s’ouvrirait dès qu’on tape les trois chiffres secrets consécutivement. Si vous avez oublié le code, la SDB B(10,3) donne la séquence qui ouvrira la porte à coup sur en pressant le minimum de touches…

On peut aussi remarquer qu’une SDB comme

B(2,8) = 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 1 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0 1 1 1 0 0 0 1 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 1 1 1 0 1 0 0 0 1 1 1 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 0 0 1 0 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 1 1 0 1 1 1 0 0 1 1 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1

, qui définit en 256 bits les 256 octets possibles en binaire (compression d’un facteur 8 par rapport à l’énumération!), se rapproche assez du code de Gray(-Gros)  connu par 1 des 10 types de mathématiciens: on passe d’un nombre à l’autre par un décalage à gauche ou à droite et l’entrée d’un seul bit d’information du côté opposé.

Retour au nombre univers compact

Dans la SDB B(10,n), tous les nombres à n chiffres ne sont représentés qu’une seule fois.

La tentation est grande de proposer comme nombre univers le plus compact qui soit un nombre dont les décimales seraient données par B(10,∞), ce qui garantirait que chaque nombre de longueur infinie n’y figure qu’une seule fois…

J’aurais même été tenté d’en écrire les premières décimales :

U=0,3 141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 …

Ben oui, comme les SDB sont cycliques, je pourrais m’arroger le droit de commencer la séquence là où commence l’infinité de décimales de Pi, par pur esprit de provocation…

Mais on n’a pas le droit de faire tout ça; manipuler les infinis mathématiques nécessite des précautions dont je suis incapable. Je vais donc me contenter d’un nombre “ "presque” " univers, tout comme l’Univers astronomique est peut-être infini, mais seule un volume fini nous est accessible : B(10,1’000’000). Dans ce très très grand nombre, il y a une seule fois le nombre formé d’un million de chiffres 5, et l’oeuvre complète de Shakespeare s’y trouve aussi, ainsi que tous les autres livres édités et pas encore écrits, ainsi que toutes les autres informations accumulées par l’humanité puisqu’elles sont en nombre largement inférieur quoique colossal. De plus, comme chaque bloc d’un million de décimales de pi, de e et des autres transcendants y figure aussi, j’ai cette fois rigoureusement le droit de commencer la séquence par le premier million de décimales de pi. 

Note* : en fait c’est fortement suspecté et Bailey et Crandall ont proposé en 2001 une démonstration de la normalité en base 2 de pi, e et d’autres “ "constantes fondamentales” " basée sur une conjecture qu’il reste à prouver. [1]

Références

1. David H. Bailey and Richard E. Crandall “ "On the Random Character of Fundamental Constant Expansions” ", Experiment. Math. Volume 10, Issue 2 (2001), 175-190.
2. “ "mots de De Brujin” " sur Jeux et Mathématiques (avec un générateur en ligne acceptant les lettres)