L'ensemble des transformations de Möbius, est le sous-groupe des homéorphismes de
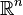généré par les inversions, c'est-à-dire l'ensemble des composées d'un nombre fini d'inversions.Les principaux exemples de transformations de Möbius sont:
- Les translations (par composition de deux réflexions)
- Les isométries de 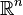(par composition de n réflexions au plus)
- Les homothéties par composition de deux inversions par rapport à des sphères puis d'une isométrie)
Ce court film dépeint la beauté mathématique des transformations de Möbius. Les séquences du film tentent de montrer que le passage à unedimension supérieure peut rendre la compréhension plus facile .
Jeu de briques
Snake
Pacman
Bubble