La physique des horizons:le pouvoir de l imaginaire et le chaos (23)

2 : LA LIMITATION INSURMONTABLE DU POUVOIR DES MATHEMATIQUES

Au-delà des problèmes intrinsèques des mathématiques que GREGORY CHAITIN a mis en exergue , je me dois de vous parler de l ultime LIMITATION , celle qui découle des équations de HENRI POINCARE sur le chaos …. Je vous préviens :mon article ne sera pas attractif pour les «  dégoûtés des maths » !

Je ne puis revenir sur les divers articles et toutes les pages nombreuses que je vous ai proposées sur le sujet

J e vais d abord me contenter d une petite réactualisation brève du sujet et vous parler de son influence en cosmologie et en physique . .

2-1 :RAPPELS

L’article dont je vais m inspirer est extrait du «  Pouvoir des mathématiques » et du ¨Pr. IAN STEWART / « Les irrégularités ont aussi leur modèle ».

Curieusement , après sa mort en 1912 , les mathématiciens et les physiciens s’étaient un peu désintéressés d un théorème fondamental de POINCARE proposé par ce dernier à l issue du défi du roi de Suède et de Norvege en 1886 sur le problème des 3 corps et la stabilité du système solaire …Après une première erreur POINCARE s aperçu qu on sortait de l implacable vision d un univers déterministe de NEWTON -LAPLACE  ; je le cite : « ..... il peut arriver que de petites différences dans les conditions initiales en engendrent de très grandes dans les phénomènes finaux ; une petite erreur sur les premières produira une erreur énorme sur les derniers. La prédiction devient impossible et nous avons le phénomène fortuit. »

Pourtant il n était pas le seul à s occuper de ce phénomène d’évolution désordonnée du monde …

En 1892, LYAPOUNOV avait étudié le problème général de la stabilité du mouvement. Il y introduisait l'idée de mesurer la divergence possible entre deux orbites issues de conditions initiales voisines. Lorsque cette divergence croit exponentiellement avec le temps pour presque toutes les conditions initiales voisines d'un point donné, on retrouve le phénomène de sensibilité aux conditions initiales….

En 1927 VAN DER POL décrit un circuit électronique de pulsation irrégulière et en 1960 SMALE trouve un système qui bien que déterministe présente certaines propriétés aléatoires 

Mais mathématiciens , astronomes , cosmologues , physiciens ont bien d autre chats à fouetter dans ce demi siècle (1900-1950) aussi excitant !

2-2 :L INVENTION DU CHAOS

Ce n'est véritablement que dans les années 1970 que le terme de « chaos » a été introduit par les deux mathématiciens Tien-Yien Li et James A. Yorke. La théorie du chaos doit en effet sa popularisation aux progrès de l'informatique à partir des années 1960-70 qui rend accessible a MR TOUTLEMONDE la visualisation directe de l'incroyable complexité de ces systèmes dynamiques. CHAOS est tout à fait le genre de terme suggestif qui stimule l imaginaire des journalistes et des media !

Il existe en fait pas mal de contributeurs  importants depuis : O.SHARKOVSKI /V.ARNOLD /E.LORENZ /S.SMALE//D.ANOSOV ETC

On réalise alors dans cette période que les systèmes chaotiques peuvent ENCORE être prédits sur le court terme mais pas sur le long terme ….

MAINTENANT ,un peu de mathématiques pour vous rafraichir les idées !

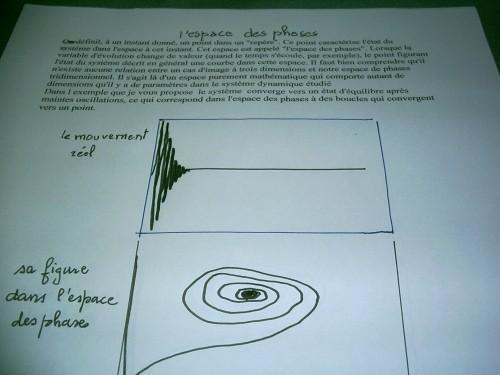
Definissons d abord ce qu on appelle l "espace des phases ": D'après les équations de la mécanique, l'évolution d'un système mobile est entièrement déterminée par la donnée initiale de la position (x, y, z) et de la vitesse (vx, vy, vz) — la masse étant connue, la quantité de mouvement est proportionnelle à la vitesse..et une equation différentielle permet de voir ou va le mobile....Vous n avez pas compris ?

.Alors je vous propose quelques photos d exemples plus explicatifs mais sachez que la résolution d une équation différentielle du premier ordre a coefficients constants ne fait pas trembler de terreur un mathématicien meme débutant !

 Cependant , pour un système chaotique, une très petite erreur ( ou imprécision) sur cette connaissance de l'état initial dans l'espace des phases va se trouver (presque toujours) rapidement amplifiée dans la résolution de cette équation ….La nouvelle trajectoire devient «  folle » !

Quantitativement, la croissance de l'erreur est localement exponentielle pour les systèmes fortement chaotiques, baptisés selon la théorie ergodique K-systèmes , ainsi que pour les systèmes très fortement chaotiques, dits B-systèmes . Le pouvoir prédictif qui découle de l'unicité de la solution de l équation différrentielle du premier ordre par rapport au temps assurée par le théorème de Cauchy-Lipschitz tombe à l eau !

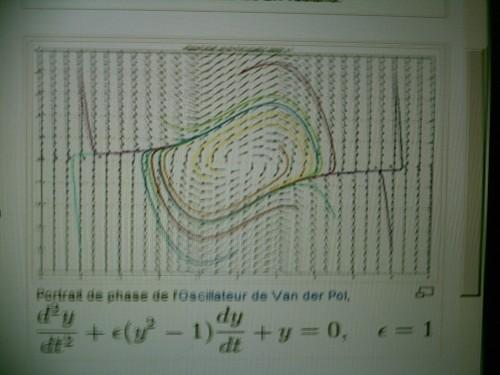
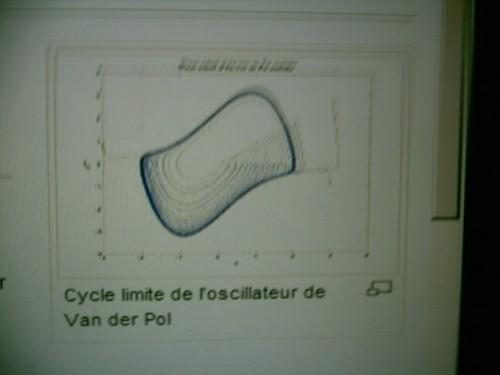
Typiquement, pour un système chaotique, les erreurs croissent localement selon une loi mathématique du type :e puissance t/τ où τ est un temps caractéristique du système chaotique, appelé « horizon de LYAPOUNOV » . l'évolution du système n’est prévisible que pour les instants ou l'exponentielle vaut encore approximativement 1, et donc tels que l'erreur garde à peu prés sa taille initiale. Dans mes articles anciens vous trouveriez le développement des notions d ergodicité et de temps de récurrence etc qui aident à mieux préciser toutes les formes possibles de chaos et de ces attracteurs qu on qualifie de ce nom mystérieux d’ étranges !….. Dans mes archives vous trouveriez des photos de courbes qui ressemblent à des coquilles de moules que la chaleur a fait ouvrir !!( attracteur de LORENTZ) 

2-3 : LE PRESENT DES MATHEMATIQUES DU CHAOS

PARLONS MAINTENANT DE PHYSIQUE ET DE COSMOLOGIE !

La description d'un système physique quantique dans l'espace des phases peut se faire de la même manière, à ceci près que le principe d'incertitude d'Heisenberg sur la position et la vitesse ne permet plus maintenant de repérer un point dans cet espace. Les incertitudes sur les coordonnées imposent donc de repérer un « point » par une tache dont l'aire est de l'ordre de h bar .Le chaos vient ensuite et se surajoute au «  flou » quantique !

Par ailleurs et plus récemment, des calculs numériques effectués par l'astronome Jacques Laskar en 1989-1990, puis confirmés par Sussman & Wisdom en 1992, ont montré que le système solaire est chaotique, avec un horizon de Lyapounov de l'ordre de 200 millions d'années. J e vous en ai parlé et vous reparlerai de l horizon de LYAPOUNOV pour une galaxie , un amas ou un univers local ETC !…

Il existe actuellement un institut de l’étude de la complexité et du chaos ! L'Institut de Santa Fe (Santa Fe Institute ou SFI) est un institut de recherche dédié à l'étude des systèmes complexes. Il se situe à Santa Fe (Nouveau-Mexique), et a été fondé par George Cowan, David Pines, Stirling Colgate, Murray Gell-Mann, Nick Metropolis, Herb Anderson, Peter A. Carruthers, et Richard Slansky en 1984. Ils étaient à l'époque tous sauf Pines et Gell-Mann scientifiques au Laboratoire national de Los Alamos. E t j aurais du aller les voir lorsque j ai visité LOS ALAMOS EN 1987 mais Santa Fe est si charmant !…….

La littérature sur le chaos et les INFORMATIONS du WEB sont pléthoriques

A suivre