La page du jeudi 18 mars 2010

Idiomathique du jour

La cuisine mathématique est toujours bien aromathisée.

Norbert Wiener 

Le mathématicien américain Norbert Wiener est mort le 18 mars 1964.
Il est surtout connu pour être le fondateur de la cybernétique (science générale de la régulation et des communications dans les systèmes naturels et artificiels).

Citations :
What most experimenters take for granted before they begin their experiments is infinitely more interesting than any results to which their experiments lead.
que Google traduit en :
Ce que la plupart des expérimentateurs tiennent pour acquis avant même de commencer leurs expériences est infiniment plus intéressant que les résultats auxquels conduisent leurs expériences.
One of the chief duties of a mathematician in acting as an advisor to scientists is to discourage them from expecting too much of mathematicians.
que Google traduit en
L'une des principales fonctions d'un mathématicien agissant à titre de conseiller auprès de scientifiques est de les décourager d'attendre trop des mathématiciens.

Auguste De Morgan 

Le mathématicien britannique Auguste De Morgan est mort le 18 mars 1871.
Fondateur avec Boole de la logique moderne, il a notamment formulé les lois de De Morgan:
- La négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions, ce qui signifie non(A et B) est (non A) ou (non B).
- La négation de la disjonction de deux propositions est équivalente à la conjonction des négations des deux propositions, ce qui signifie que non(A ou B) est (non A) et (non B).
ou pour être plus concis et peut être plus clair :


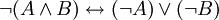
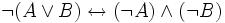
Citations :

- Le moteur de l'invention mathématique n'est pas le raisonnement 
mais l'imagination.
- Quand on lui demandait son âge, il répondait : 
j'avais x ans en l'an x².
- Imaginez une personne qui n'a pas peur du ridicule. Elle
pourrait vous dire : premièrement, un nombre négatif n'a pas
de logarithme; deuxièmement, un nombre négatif n'a pas de racine
carrée; troisièmement, le rapport entre ces deux nombres qui
n'existent pas est égal au rapport entre la circonférence et le
diamètre d'un cercle.

Jakob Steiner, un mathématicien romantique ? 

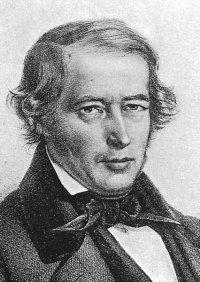
Le mathématicien suisse Jakob Steiner est né le 18 mars 1796.
Ses travaux mathématiques concernent essentiellement la géométrie.
On lui doit le joli théorème de Poncelet-Steiner selon lequel tout point constructible à la règle et au compas peut être construit uniquement à l'aide de la règle à condition que soit tracé dans le plan un cercle avec son centre.
On connait aussi l'arbre de Steiner problème d'optimisation qui a inspiré un sujet pour l'épreuve pratique du bac S (sujet 3 en 2007).
Le texte "Jakob Steiner, un mathématicien romantique ?" (fichier pdf) d'Anne Boyer, tiré des Actes du colloque de Peyresq (1999) "La pensée numérique", permet de mieux connaître Steiner. On y découvre son éducation, ses idées pédagogiques, son comportement plus ou moins asocial et sa pensée mathématique.
Une citation de Steiner issue de ce texte :
"La méthode employée à l'institut de Pestalozzi, consistant à traiter les vérités mathématiques comme des sujets de libre réflexion, m'a amené, alors que j'étais élève, à chercher si possible, à la place des proposition avancées pendant l'instruction, d'autres propositions qui fussent plus profondes que celles que présentaient les professeurs, et bien souvent, j'y arrivais si bien, que les professeurs préféraient mes démonstrations aux leurs."
Le texte d'Anne Boyer se termine par cette phrase étrange :
"Le vieux Jacob Steiner se plaignait à son ami Shläffi de sa fatigue qui l'empêchait de travailler car « lorsqu'il fermait les yeux pour voir, il s'endormait »."
Le secret de la géométrie serait donc de savoir observer les figures en fermant les yeux.
On peut y voir la réflexion provocatrice d'un surdoué (comme Euler), mais aussi l'idée que l'observation, si elle n'est pas accompagnée d'une certaine réflexion, ne mène pas très loin.
Pour terminer, voici un petit exercice :
Fermez les yeux. Vous voyez apparaître un cercle avec son centre, une droite d qui coupe le cercle et un point P. Comment tracer la perpendiculaire à d passant par P en n'utilisant qu'une règle qui est évidemment non graduée ?
C'est possible d'après le théorème de Poncelet-Steiner, toute la difficulté est d'y arriver avant de s'endormir.
On peut aussi aller voir ici...

Christian Goldbach et sa conjecture 

Le mathématicien allemand Christian Goldbach est né le 18 mars 1690.
Il est célèbre pour avoir formulé la conjecture de Goldbach: tout nombre entier pair strictement supérieur à 2 peut être écrit comme la somme de deux nombres premiers.
Cette conjecture, qui s'exprime en termes simples, n'a toujours pas été démontrée; elle inspire cependant les romanciers :
- Les obstinations d'un mathématicien, de Didier Nordon
- Oncle Petros et la conjecture de Goldbach, d'Apostolos Doxiadis

Philippe de La Hire 

Le mathématicien, physicien et astronome français Philippe de La Hire est né le 18 mars 1640.
On peut lire l'Eloge de Philippe de La Hire par Fontenelle dans son histoire de l'Académie des Sciences (fichier pdf).
Continuateur de Girard Desargues et de Blaise Pascal il déduit les propriétés des coniques à partir des propriétés du cercle. Il innove en ce qu'il exploite au maximum les propriétés d'invariance de la division harmonique. On peut lire à ce sujet sa "Nouvelle méthode en géométrie pour les sections des superficies coniques et cylindriques..." sur Gallica.
La Hire a aussi laissé son nom à la droite de La Hire ou au théorème de La Hire.