Max DD - Money Management, suite

On repart du jeu 1 (voir billet précédent) afin de simuler la perte maximale probable que le joueur aurait pu constater avec un taux de réussite de 80%.
On modifie une donnée : le jeu devient infini (il ne s’arrête plus à 50 coups) et rien ne garantit au joueur de constater de manière certaine un taux de réussite de 80% à l’issue des 50 premiers coups.
Ce changement est fondamental car le joueur se retrouve dès lors dans un environnement risqué : il sait que le jeu 1 lui procure un taux de réussite historique de 80% mais il ignore quel sera l’ordre de sortie des coups gagnants et perdants… (vous constaterezz que l’on se rapproche du trading).
Nous avions déterminé que le risque optimal (fraction optimale du capital à engager) qui permettait de maximiser les gains du jeu 1 après 50 coups était de 40%.
De manière très concrète, risquer 40% du capital à chaque coup fait courir au joueur le risque de constater une réduction importante de son capital en cas de coups perdants successifs.

• 3 coups perdants successifs engendrent une réduction du capital de : ((1-0.4)^3) -1 = -78.4%
• Parallèlement la probabilité de constater 3 coups perdants successifs est de (1-0.8)^3 = 0.8%

Pour certains joueurs plus averses au risque que d'autres, une telle réduction du capital en 3 coups n'est pas supportable : ceux-ci réduiront leur risque mais réduiront également le rendement du jeu en contrepartie…

En utilisant la loi binomiale, on peut déterminer quel sera la perte maximale probable du joueur à l’issue de la xème transaction.

Cette perte maximale probable est fonction de quatre éléments au moins :

1. Le taux de réussite du jeu (fonction négative : plus le taux de réussite est élevé, moins les draw down seront importants)
2. Le rapport gain/perte (fonction négative)
3. La fraction du capital engagée à chaque coup (fonction positive : plus la fraction du capital engagée est forte, plus le drawn down sera important
4. L'ordre des coups gagnants et perdantes
   

Le graphique ci-après montre l'évolution du capital à l’issue de chaque coup pour le jeu 1, avec un niveau de risque optimal calculé à 40%. Il y a trois courbes qui représentent 3 niveaux de perte maximale probable.

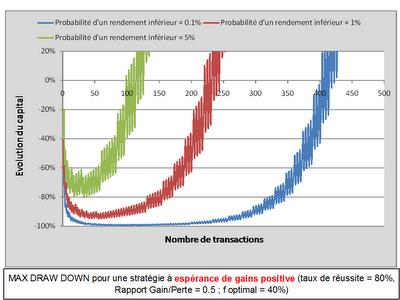
• La courbe haute représente la perte maximale probable à l’issue de chaque coup : dans 95% des cas, le capital du joueur est au-dessus de cette courbe.
• La courbe intermédiaire représente la perte maximale probable à l’issue de chaque coup : dans 99% des cas, le capital du joueur est au-dessus de cette courbe.
• La courbe basse représente la perte maximale probable à l’issue de chaque coup : dans 99,9% des cas, le capital du joueur est au-dessus de cette courbe.

Ce graphique montre que pour un jeu à espérance de gains positive, le capital finit toujours par croitre : le temps joue toujours en la faveur du trader (comme le temps joue toujours en la faveur du casino face au joueur de casino).

Le second graphique reprend les données du premier, mais avec un risque moins fort (f=10% contre 40% précédemment) qui a pour effet de réduire les niveaux de perte maximale. Naturellement, la décroissance du capital est plus faible... puisque le risque est plus faible. La contrepartie (qui ne se voit pas sur ce graphique) est un rendement moyen moins important.

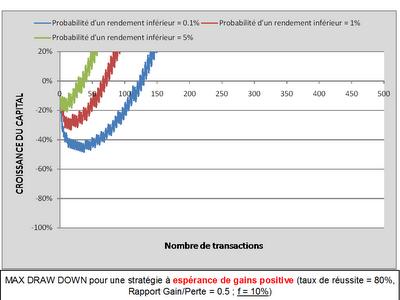
Ces deux graphiques démontrent quelque chose d'extrêmement important : les points bas d'un jeu à espérance de gains positive sont atteints dans la première partie de vie du jeu... C'est là qu'il faut tenir et ne pas décourager.

Lien avec le trading :

La démonstration précédente peut s’appliquer aux stratégies de trading sous certaines conditions.

La loi binomiale qui est utilisée s’applique parfaitement mais imparfaitement au trading. En effet, en trading, la probabilité pour qu’une transaction soit gagnante ou perdante n’est pas constante d’une transaction à l’autre. L’utilisation de la loi binomiale pour modéliser la perte maximale d’une stratégie de trading est d’autant plus imprécise que la probabilité de réussite varie fortement d’une transaction à l’autre.

Il est bien évident qu'un trader qui n'a aucune consistance au niveau de son ratio gain/perte ne peut pas appliquer la loi binomiale pour ce type de simulation.

Un trader qui, sur une transaction va chercher un ratio gain/perte de 5 et l'autre transaction un ratio gain/perte de 0.3 ne pourra utiliser la loi binomiale.

En revanche, un trader consistant qui va chercher un ratio gain/perte voisin de X pour l’ensemble de ses transactions pourra utiliser la loi binomiale pour modéliser sa perte maximale probable.

Edouard Martin
www.trendis-yourfriend.com