La page du jeudi 18 février 2010

Idiomathique du jour

Un disque dur ne gère des données numériques qu'après formathage.

Eugène Beltrami

Le mathématicien italien Eugène Beltrami est mort le 18 février 1900.
Dans son article intitulé "Essai d'interprétation de la géométrie non euclidienne", il exhiba un modèle concret de la géométrie non euclidienne de Lobatchevsky et János Bolyai et la relia à la géométrie riemannienne. Le modèle de Beltrami consiste en une pseudosphère (aussi appelée surface de Beltrami), surface engendrée par révolution de la tractrice autour de son asymptote.
On pourra consulter les pages consacrées à la peudosphère sur cabri.net.

Sophus Lie

Le mathématicien norvégien Sophus Lie est mort le 18 février 1899.
On lui doit la création de l'algèbre de Lie, ainsi que des groupes de Lie.
Le livre de Arild Stubhaug "Sophus Lie, une pensée audacieuse" (Springer 2005 - 567 pages) en donne une biographie détaillée. On peut le feuilleter sur Google-Livres ou le commander sur amazon.
Citations :
-Si la vie est complexe, c'est parce qu'elle a une partie réelle et une partie imaginaire.
- De nos jours, ce sont nos poètes qui impressionnent le vaste monde par leur pensée audacieuse et leur style brillant. Ne prenez pas en mauvaise part que je réclame un peu du même sang. Sans imagination, on ne devient jamais mathématicien et ce qui m'a donné une place parmi les mathématiciens de notre temps, malgré mon manque de connaissances et de style, ce fut l'audace de la pensée.

Charles Gustave Jacob Jacobi

Le mathématicien allemand Charles Gustave Jacob Jacobi est mort le 18 février 1851.
Il a surtout étudié les fonctions elliptiques qui sont d'une importance capitale en physique mathématique. Il est le premier à appliquer ces fonctions elliptiques à la théorie des nombres.
Dans une lettre du 2 juillet 1830 adressée à Le Gendre, C.G.J. Jacobi écrit:
"M. Fourier avait l'opinion que le but principal des mathématiques était l'utilité publique et l'explication des phénomènes naturels; mais un philosophe comme lui aurait dû savoir que le but unique de la science, c'est l'honneur de l'esprit humain, et que sous ce titre, une question de nombres vaut autant qu'une question du système du monde."

Leon Battista Alberti

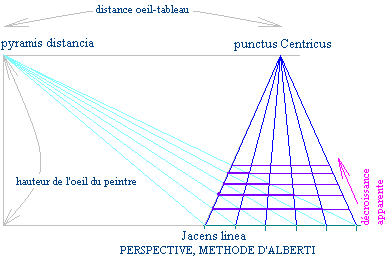
Le théoricien de la peinture et de la sculpture italien de la Renaissance Leon Battista Alberti est né le 18 février 1404.
Il nous a donné une belle méthode de construction de la décroissance de la profondeur apparente des carreaux lorsque l'on s'éloigne de la ligne de terre, en perspective.

Nasir al-Din al-Tusi

Le philosophe, mathématicien, astronome, théologien et médecin perse Nasir al-Din al-Tusi est né le 18 février 1201.
Il est considéré comme l'un des fondateurs de la trigonométrie et a réalisé la première publication des principes complets de la trigonométrie plane et sphérique.
Le système planétaire qu'il avait imaginé était le plus avancé de son temps et fut utilisé de manière intensive. Entre Ptolémée et Copernic, il est considéré comme le savant le plus éminent sur ce sujet.

Thabit ibn Qurra et les nombres amicaux

L'astronome, mathématicien et musicologue arab Abu'l Hasan Thabit ibn Qurra' ibn Marwan al-Sabi al-Harrani, mieux connu sous le nom de Thabit ibn Qurra, ou sous le nom latin de Thebit, est mort le 18 février 901.
Ses travaux de traduction des Eléments d'Euclide l'ont amené à étudier les nombres amicaux: couples d'entiers tels que chacun d'entre eux est égal à la somme des diviseurs propres de l'autre.
Exemple : Les diviseurs propres de 220 sont 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 et 110; leur somme est 284. Les diviseurs propres de 284 sont 1, 2, 4, 71 et 142; leur somme est 220. Les nombres 220 et 284 sont donc des nombres amicaux.
Rechercher ces couples d'entiers est un bon exercice de programmation.
Thabit ibn Qurra a montré comment on pouvait construire des couples de nombres amicaux en utilisant des nombres du type 3*2^n-1 qu'on appelle nombres de Thebit en son honneur.
Thabit ibn Qurra est aussi connu, en mathématiques, pour une démonstration du théorème de Pythagore sous forme de puzzle qu'on peut trouver sur le site MIAM ou sur le site Mathématiques magiques.