Cas d'une boule

Prenons le cas non plus d'un disque, mais d'une boule, nous allons voir que le résultat est semblable sur le fond.
Dans le cas d'une boule la masse homogène s'écrit : M(r) = M0.r^3/r0^3, c'est la seule chose qui change ! Et donc tout simplement on a :
(r<r0) dt1 = racine (1-r2.Rs0/r0^3).dt2
(r>r0) dt1 = racine (1-Rs0/r).dt2
La seule chose qui change vraiment c'est donc à l'intérieur de la boule de matière où le facteur r2/ro^3 remplace r/r0^2, ce qui donne pour l'histoire de l'effondrement de la boule ceci pour les sphères temporelles :

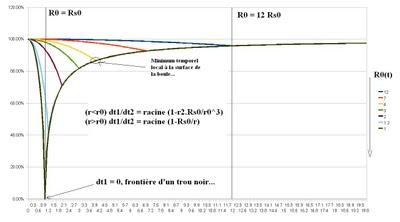
Voyez comme à la surface de la boule, au fur et à mesure que son rayon R0 tend vers son rayon de Scharzschild, le temps sur cette surface tend vers zéro... Que peut bien signifier physiquement (et spirituellement ?! ...) un temps qui s'annule ? En quoi cette propriété remarquable joue sur les équilibres dynamiques de l'Univers ? Comment interpréter ce phénomène si l'on change de référentiel accéléré et donc d'horloge ? Est-ce qu'un temps relatif pourrait s'annuler pour un observateur mais pas pour un autre, qu'est-ce que cela signifie sur la nature même des objets massifs, classiques ou quantiques ? Cela permet-il d'envisager une fusion conceptuelle globale à partir de ce concept ?
Une série palpitante aux frontières de l'esprit de la matière et de l'Univers, à suivre sur ce blog... :)
C'est quoi au fait une boule qui s'effondre comme ça ? C'est simplement une étoile qui se transforme en trou noir (si elle passe sous Rs0 en rayon, elle devient trou noir)...