Problème de planification d’horaire (2e partie)

Le premier article de cette série décrivait la problématique de la planification d’horaires. Il a été publié il y a quelques mois de cela sous le titre: Problème de planification d’horaire.

Couverture d’une courbe des besoins
La couverture d’une courbe de besoins est en fait le problème que l’on résout lorsque l’on optimise des horaires,  ce qui suit la décrit. Chaque quart de travail (shift) est caractérisé ici par son heure de début et son heure de fin, et l’objectif est de choisir le nombre d’employés à faire travailler sur chaque quart, de façon à couvrir les besoins tout en minimisant le nombre total d’heures de travail pour cette journée. Le problème est donc polynomial. De plus, les différentes contraintes de la vie courante d’une compagnie rendent le problème de plus en plus compliqué.

Exemple :

Dans cet exemple, on présentera la couverture d’une courbe des besoins. On a quatre quarts Q1, Q2, Q3 et Q4, et une table des besoins décrite ci – dessous :

Tableau 1 : Table des différentes quarts de travail

Les quarts

Heure de début

Heure de fin

Q1

8H

12H

Q2

12H

16H

Q3

14H

16H

Q4

16H

20H

Tableau 2 : Table des besoins

Horaire

8H-12H

12H-14H

14H-16H

16H-20H

Besoins

5

10

12

3

Couverture d’une courbe de besoin par les Quarts de notre exemple

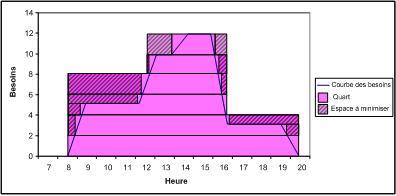
Dans la figure précédente, on a placé les différents quarts Q1, Q2, Q3 et Q4 sur la courbe de besoins. On essaie de couvrir la courbe de besoins tout en minimisant la partie des quarts qui se situe à l’extérieure de l’intersection des quarts et de la courbe (la partie hachurée).

Donc l’objectif consiste à minimiser l’écart entre les besoins et les quarts affectés.

Min ∆= min (∑ des besoins – ∑ des quarts placés).

À condition que ∆ ≥ 0.

Les méthodes de résolution seront évoqués dans une troisième partie.