Vitesse et stabilité

La question du temps, même si ce n’est pas trivial à première vue, est centrale en biologie, et particulièrement en évolution. Le grand Slobodkin, en 1961, a différencié le temps écologique (une dizaine de générations) et le temps évolutif (une centaine de générations). Dans la plupart des cas observables à l’observation directe (les grosses bêtes), c’est vrai. Mais que se passe t-il quand les deux temps se rapprochent?

Si les temps écologiques et évolutifs sont découplés, on s’attend à ce que les processus écologiques soient parfaitement prédictibles, et que l’évolution n’agisse pas tellement : les systèmes peuvent atteindre un équilibre sans trop de difficultés. Ce qui fait la différence entre temps écologique et temps évolutif, c’est la différence qui existe entre le temps d’une interaction et le temps d’une génération. Si vous vous reproduisez une fois tous les dix ans, et interagissez toutes les 20 minutes, votre écologie, au moment de l’observation, est peu dépendante des phénomènes évolutifs. Si, en revanche, vous interagissez toutes les 20 minutes, et avez un temps de génération de 40 minutes, les deux temps convergent.

C’est tout à fait le cas des bactéries et de leurs virus (ou autres prédateurs à temps de génération court). Qu’est-ce que l’évolution rapide va faire sur les systèmes?

Considérons le système le plus simple qu’on puisse imaginer : un système proie-prédateur obéissant aux équations de Lotka-Voltera (ou p est le nombre de proies et P le nombre de prédateurs – intégré avec la méthode de Runge-Kutta quatrième ordre, code R dispo pour ceux qui veulent) :

dp/dt = p * ( a - b*P )
dP/dt = -P * ( g - d*p )

Si on simule ce système avec des paramètres classiques (0.2 pour tous les paramètres, p = 1, P = 0.9), on observe des oscillations classiques :

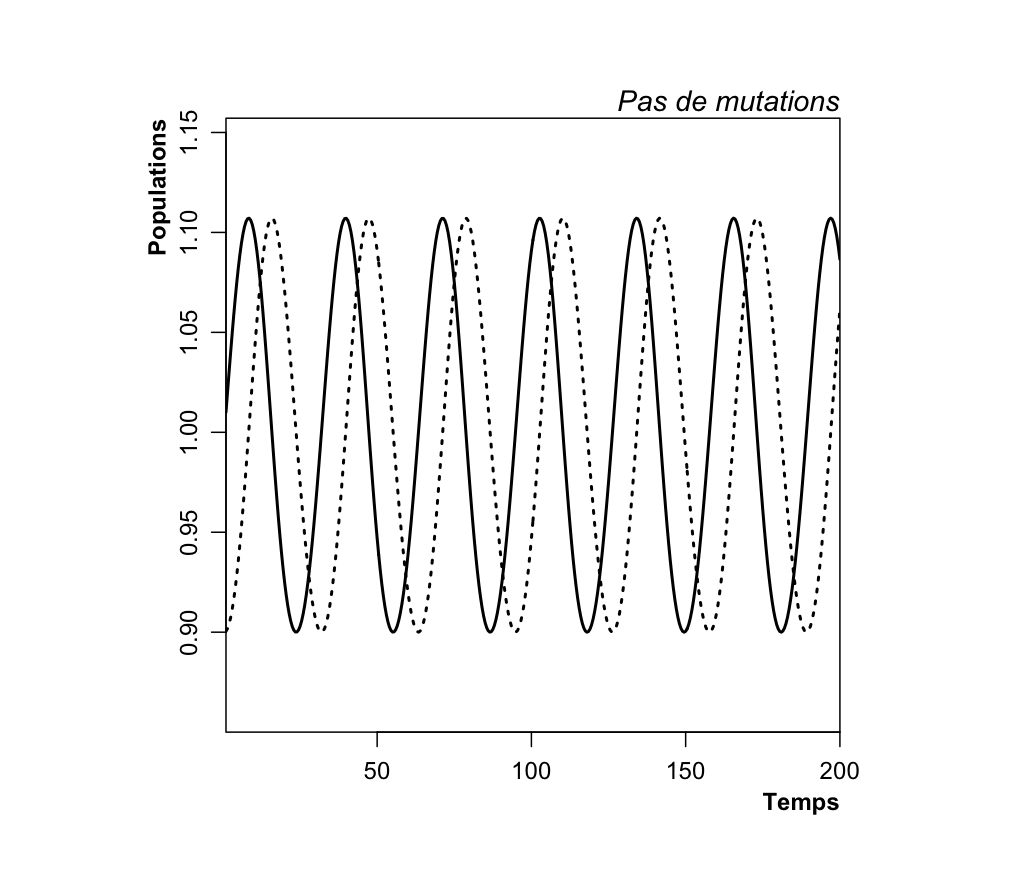
Si on ajoute des mutations (sur les paramètres a, b, g, et d) à une fréquence faible, la dynamique n’est pas nécessairement très différente :

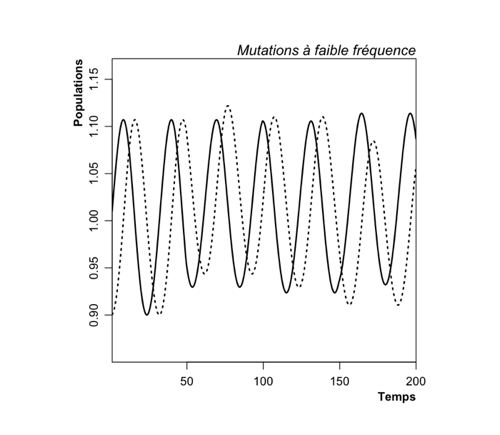
On voit qu’une autre dynamique se superpose (les extrema locaux ne sont pas identiques d’une oscillation à l’autre), mais rien de déstabilisant. Si maintenant on augmente un peu la fréquence de mutation (vous aurez compris que c’est mon proxy pour la vitesse évolutive), on voit une toute autre dynamique se mettre en place :

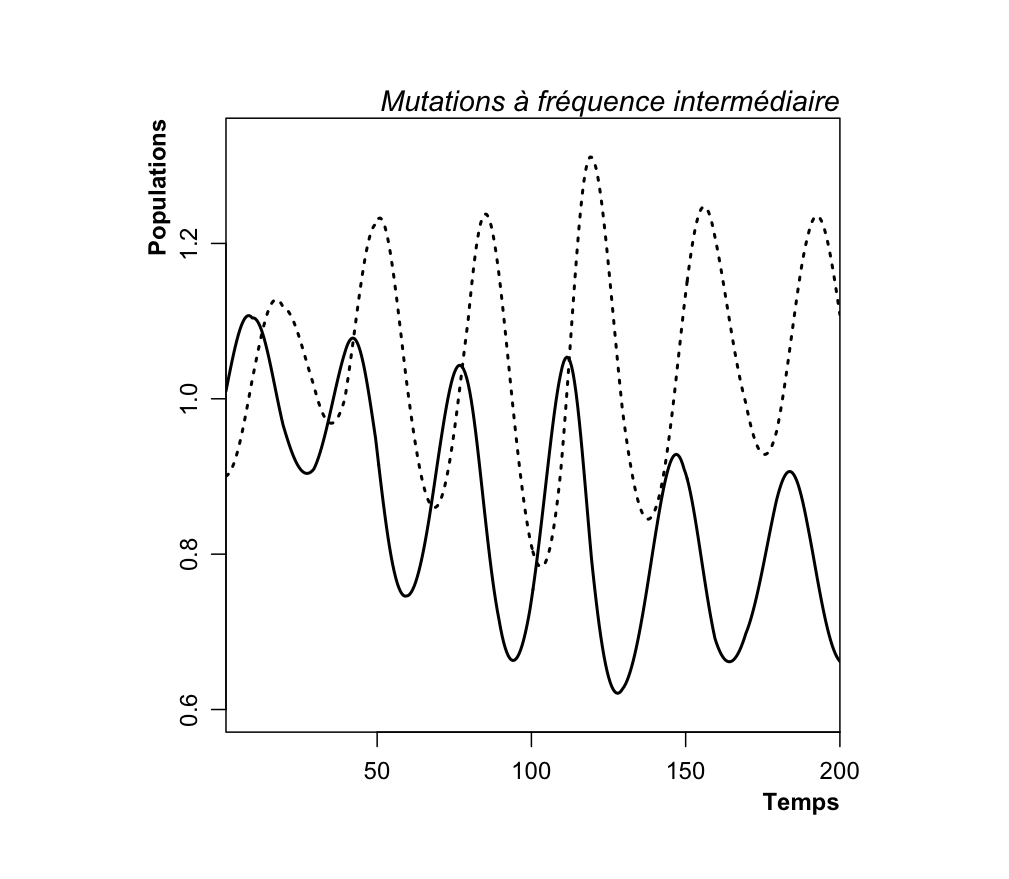
On déplace la valeur autour de laquelle on oscille, et la fréquence des oscillations varie un peu (faites moi confiance, j’ai vérifié). On entre dans une situation de feedback : l’évolution va “nourrir” l’écologie, en modifiant les dynamiques temporelles.

Si enfin on considère que les mutations sont quasi permanentes, on finit par déstabiliser complètement le système :

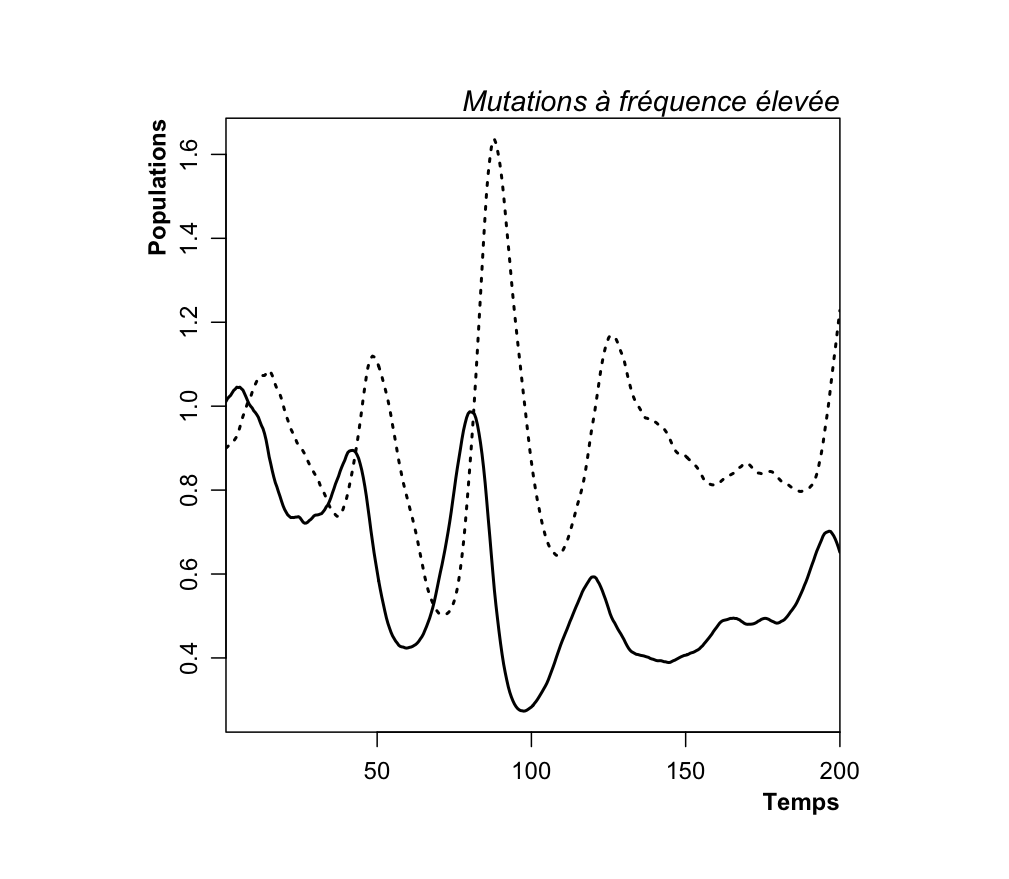
Ce qui détermine la dynamique temporelle des espèces n’est plus uniquement leur écologie, mais aussi la vitesse à laquelle elles évoluent.

On peut reprocher à mon modèle de considérer que toute la population mute en même temps (pas de spéciation, pas de branching). J’avais fait le test en n’autorisant que les souches meilleures que leurs ancêtres à envahir, et on observe évidemment les même patterns.

Bref, vous l’aurez compris, ce billet voulait seulement vous rappeler que je n’ai pas oublié que ce blog existe, et en passant vous faire prendre connaissance d’une partie de mes intérêts du moment…

Billets similaires