La résistance, puisqu’il est vain d’espérer me voir commencer une note sur autre chose que des généralités bien senties, est la capacité qu’a un organisme a résister à un autre. Cette notion est en général utilisée dans le cas des relations entre les hôtes et les parasites.
Le trait de résistance est soumis, comme tous les autres traits, à évolution. Et dans un système hôte-parasite, il existe un “contre trait” du parasite (l’infectivité) qui évolue en retour.
Dans sa théorie de la Reine Rouge, Leigh Van Valen nous apprend qu’en situation de course aux armements, l’évolution des défenses des hôtes (la résistance) évolue en réponse à l’évolution des contre-défenses (l’infectivité) des parasites (qui ont un temps d’avance dans la coévolution, mais nous parlerons de ça plus tard).
Plus un parasite va devenir infectieux, plus on va sélectionner pour des hôtes résistants (on court de plus en plus vite, en couvrant de plus en plus de distance, dans le seul but de rester sur place). Est-ce toujours vrai? Existe-t-il des cas pour lesquels la résistance devient superflue, et pour lesquels l’hôte peut laisser tomber et retourner à un état de sensibilité à un parasite hyper-virulent?

Si on prend uniquement la théorie de Van Valen, c’est peu probable. Mais si je permet de perdre votre précieux temps à poser la question, c’est évidemment pour y répondre positivement…
Dans la vie, et ce sera le paragraphe de philosophie de comptoir de ce billet, on n’a rien pour rien, et tout se paie. Imaginons un système génétique dans lequel H et P (hôte et parasite) portent chacun k loci (des emplacements dans leur génome), qui peuvent être soit dans l’état 0 (absence du trait – résistance ou virulence), soit dans l’état 1 (présence du trait).
Un parasite qui porterait 01001 serait donc infectieux sur deux loci, et avirulent sur trois autres. De la même manière, un hôte qui porte 11111 est entièrement résistant. D’après Van Valen, au moins en première lecture, on tend vers la situation suivante :
P 11111 (total : 5) H 11111 (total : 5)
C’est-à-dire, une résistance/infectivité maximale.
Imaginons maintenant que tout se paie, et que ce qu’on gagne en résistance (les 1 supplémentaires) soit perdu ailleurs (par exemple en capacité métabolique – G). Supposons même qu’on connaisse la formule, et qu’en suivant l’exemple de Steve Frank, on écrive que G = G0(1-c)n, avec G0 la capacité métabolique de base, n le nombre de loci portant un 1, et c le coût “net” qu’on paie à chaque fois qu’on porte 1 sur un locus.
Le déficit D subi [ (1-c)n ] est donné dans le graphique suivant (n est en abscisses, D en ordonnées) :
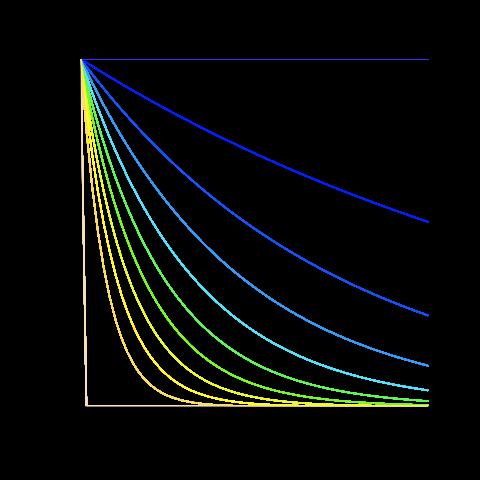
Plus on est proche du bleu, plus c est proche de 0. Plus on approche du beige, plus il est proche de 1. Pour des coûts élevés, comme la première courbe verte, porter 2 sites résistants, c’est perdre 75 % de sa capacité métabolique!
Dans la vision classique de Van Valen, donc, la coévolution risque de faire évoluer vers des coûts maximaux, et ça devient désavantageux. Est-il possible que dans certains cas, l’hôte décide de laisser tomber la résistance, parce qu’il perd trop en fitness? Oui!
Pour un système avec 5 loci, on peut obtenir (dans certains conditions que je ne détaille pas) une évolution du nombre moyen de sites portant la résistance (ou la virulence) comme celle qui est représentée ci-dessous :
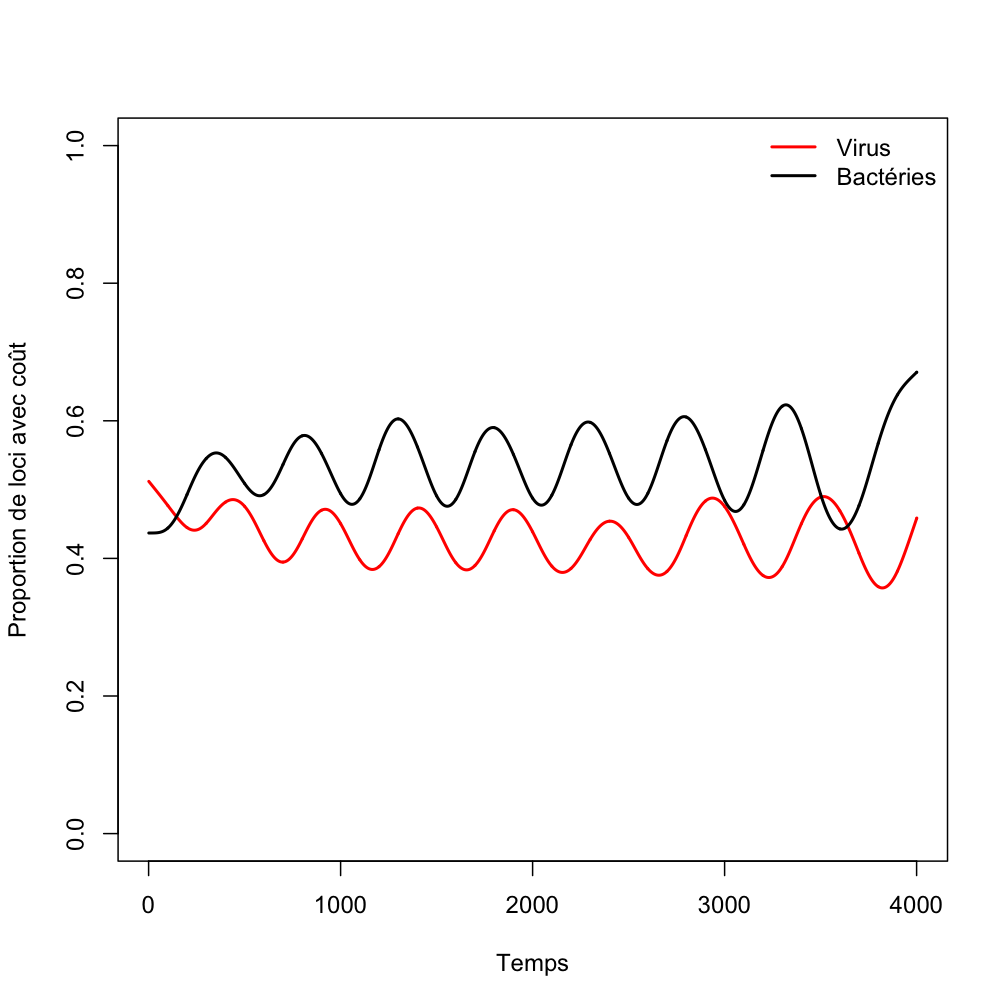
Vous remarquerez que dès que le parasite devient très virulent (crêtes de la courbe rouge), l’hôte commence à se laisser faire et perd des sites de résistance. Quand l’hôte commence à perdre en résistance, le parasite perd en virulence (qui n’a plus grand intérêt), et le cycle continue. Comme vous pouvez le voir, cette cyclicité est même assez harmonieuse :
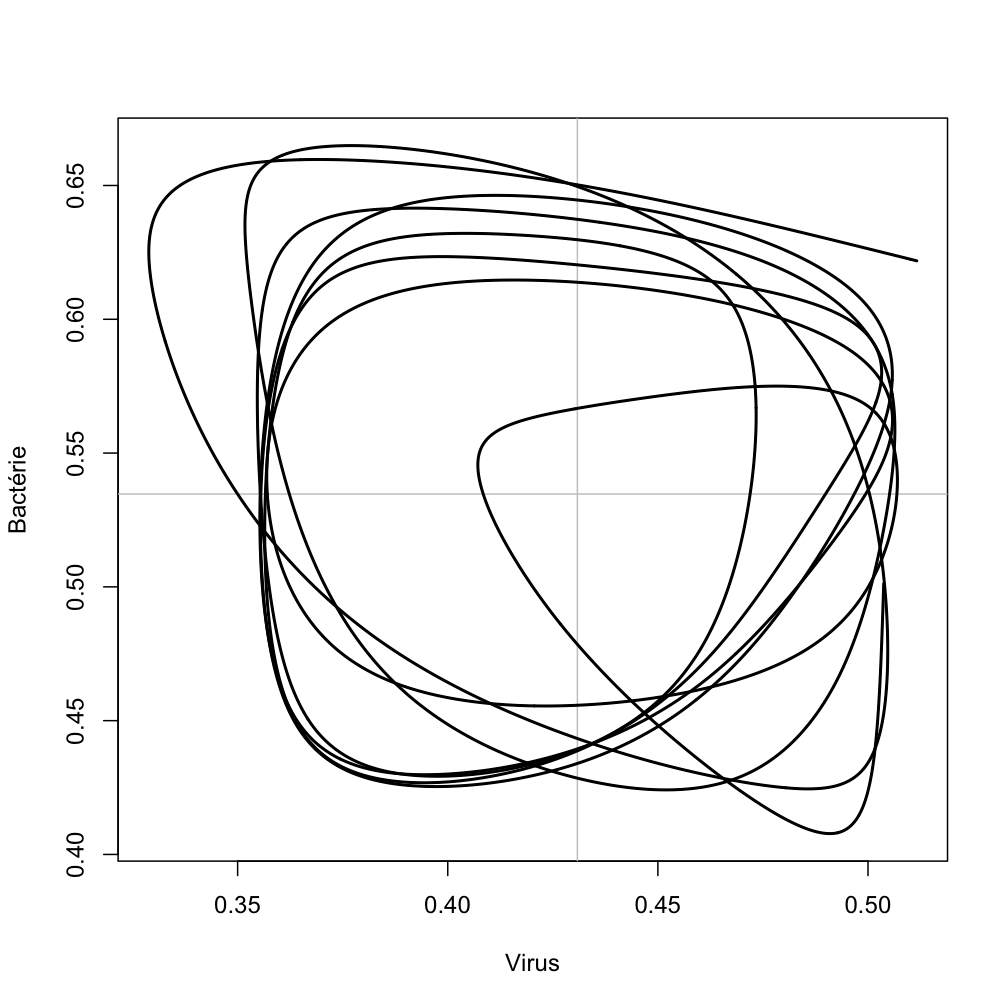
A part dans les toutes premières étapes, ou le signal évolutif est perturbé par l’évolution rapide de la dynamique de population (et inversement par la suite!), on va osciller autour du point d’intersection des deux droites grises, qui correspond… à la moyenne du nombre de sites de résistance/virulence portés au cours de la simulation!
Le take-home message de cette note est donc que la virulence maximale (et la résistance maximale) n’est pas nécessairement atteinte, et que si les deux antagonistes d’une course aux armements courent de plus en plus vite, ils peuvent ne pas courir en ligne droite…
