Quizz #4 : mais c’est quoi donc?

Dans l’optique de vous faire croire que j’ai la moindre seconde a consacrer à ce blog - vaine tentative! -, un petit quizz qui, je dois l’avouer, va favoriser les écologues et populationnistes (ce mot n’existe pas, je pense) de l’asemblée.

En ne limitant surtout pas votre imagination, essayez de me dire à quoi correpond l’image suivante :

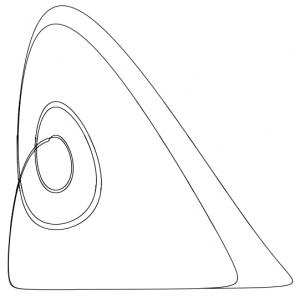
Qu’est-ce que ça représente, qu’est-ce que ça veut dire, comment on l’obtient…? A vos claviers!

La solution

OldCola, Tom Roud, et Coincoin ont chacun apporté un élément de la réponse : il s’agit de la représentation de la population d’une communauté de parasites et d’une communauté de leurs hôtes (chaque communauté se composant de plusieurs génotypes, avec de la spéciation et des extinctions) au cours du temps. Les perturbations qu’on observe sont liées à la “remise à zéro” de l’écosystème à l’approche du point d’équilibre, et a un changement des conditions de l’interaction (modification des traits d’histoire de vie). Je n’en dis pas plus pour le moment.

Pratiquement tous ceux qui ont avancé une hypothèse ont parlé de Lotka-Volterra. C’est quoi donc? Tout simplement un système d’équations différentielles très simple, qui régissent le comportement d’une proie et d’un prédateur.

En gros,

p = p(a - m*P)

P = P(b*p - d)

Avec p le nombre de proies, P le nombre de prédateurs, a la capacité de croissance des proies, m la mortalité des proies liée à la prédation, b le taux d’exploitation des proies par les prédateurs, et d la mortalité naturelle des prédateurs.

Si on simule tout ça, la cinétique de la population est la suivante :

On remarque le décalage d’un quart de période (les prédateurs sont en rouge).

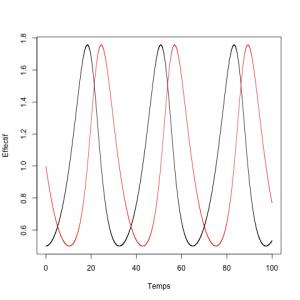
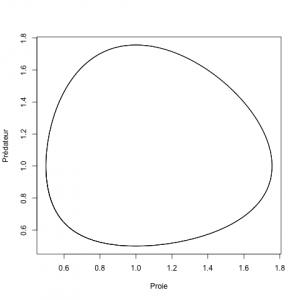
Si on représente les effectifs l’un contre l’autre, on obtient la dynamique suivante:

Ce qui correspond à une dynamique stable : on ne converge pas vers un point d’équilibre, mais on reproduit toujours le même motif dans le temps. C’est principalement la forme des équations (et pour des modèles plus complexes, l’architecture génétique) qui va déterminer si on converge vers un point stable, ou si on maintient une dynamique stable. Des cas de dynamique instable se manifestent par un cycle peu régulier, peu harmonieux, contrairement aux exemples présentés ici.

Billets similaires