Le chemin le plus court - un peu de réflexion (2)

J'avais posé une (petite) énigme lors du précédent billet, quel est le chemin le plus court pour un cavalier pour aller de A vers B sachant qu'il doit emmener son cheval boire à la rivière en chemin (figure 1, en vignette) ? Réfléchissez-y avant de lire la suite.

---

Mes fidèles lecteurs se sont déchaînés, et ont donné la solution (projeter le symétrique de A ou de B, cf. figure ci-dessous), même plusieurs solutions, en commentaires du précédent billet. J'avais ma démonstration, elle est basée sur les deux mamelles du taupin, les coordonnées cartésiennes et le calcul différentiel. C'est lourd, inélégant (je préviens), mais à mon sens convaincant.
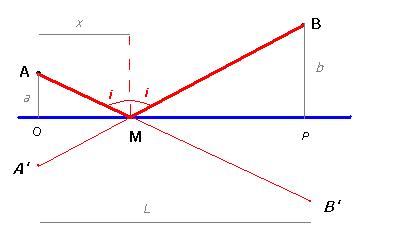
On prend pour origine du repère cartésien le point O (le milieu de AA'), par commodité.
La distance AB = AM + MB = [x² + a²]^1/2 + [(L-x)² + b²]^1/2 ; quand on dérive par rapport à x (choix du plus court chemin), on obtient l'annulation de la dérivée pour :
x  / [x² + a²]^1/2= (L-x) / [(L-x)² + b²]^1/2 ou plus simplement OM / AM = PM / BM, ce qui exprime que les triangles AOM et BPM sont semblables, donc l'égalité des angles AMO et PMB, avec deux conséquences :
1) A'M (A' symétrique de A) est aligné à MB, donc la solution est bien celle où on construit le symétrique de A par rapport à la rivière (ou de B, ce qui est strictement équivalent)

2) égalité des angles i (figure) faits avec la normale côté A et côté B : on retrouve la loi de la réflexion de Snell-Descartes - Ce n'est pas seulement le plus court chemin pour le cavalier, c'est le plus court chemin pour la lumière réfléchie... Encore de la physique qui se cache derrière une récréation mathématique !
Quand je vous disais (cf. le titre de mon premier billet) qu'il fallait un peu de réflexion....