Classement des Joueurs de Tennis (suisses)

Dans les commentaire de l’article “Le comptage des points au tennis“, un jeune joueur m’a soumis un joli casse-tête : le règlement de swisstennis sur le classement des tennis(wo)man à croix blanche. Il semblerait que ceux qui n’ont pas de bonnes bases en maths (*) aient un peu de peine à le comprendre, et c’est vrai que c’est le premier règlement sportif dans lequel je vois des formules de ce genre :

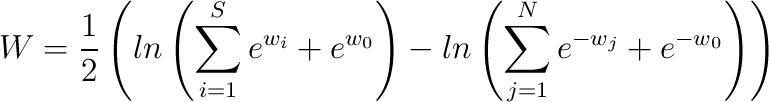
Le principe est simple:”La valeur de classement d’un joueur C est déterminée par un nombre de points précis arrondi à un millième. C représente la somme de la valeur de compétition W et de la bonification de match R.” (Art 5.1)

Un joueur qui entre dans le classement reçoit un W=1, puis “La valeur de compétition W est calculée sur la base des résultats obtenus pendant la dernière année.” (Art 5.3) en utilisant la grosse formule ci-dessus ainsi:

• w0 est l’ancienne valeur de compétition du joueur
• les wi sont les valeurs de compétition des S joueurs battus pendant l’année
• les wj sont les valeurs de compétition des N joueurs qui l’ont battu pendant la même période.

Simplifions tout ça en imaginant que Roger Federer , qui a un W=17.394, et notre jeune joueur qui en est à W=0.892 ne jouent qu’un seul match en 2009, dans lequel ils s’affrontent dans un duel sans pitié. Ainsi les sommes notées avec le Σ ne correspondent qu’au seul adversaire affronté, soit comme vaincu soit comme vainqueur.

Il est très probable que Federer gagne. Dans ce cas, selon la formule, son nouveau W vaudra (ln(exp(17.394)+exp(0.892))-ln(exp(-17.394)))/2 = 17.394000034. La magie des fonctions exponentielles et logarithmiques permet de traduire en mathématiques le Cid : “A vaincre sans péril, on triomphe sans gloire” : le classement du no.1 ne s’améliorerait pas.

Quant à notre jeune joueur, après sa défaite son W passerait à W=(ln(exp(0.892))-ln(exp(-0.892)+exp(-17.394)))/2 = 0.891999966, donc resterait inchangé après arrondi au millième.

Mais si nous avions là un génie de la raquette qui parvenait à terrasser “Rodjeur”, son W monterait à (ln(exp(0.892)+exp(17.394))-ln(exp(-0.892)))/2 = 9.143 d’un seul coup alors que Federer dégringolerait à W=(ln(exp(17.394))-ln(exp(-17.394)+exp(-0.892)))/2=9.143 aussi. Heureusement pour lui, il pourrait invoquer l’Art 5.5 qui lui permettrait de rayer cette défaite humiliante s’il avait joué au moins 5 autres matches dans l’année…

En passant, 9.143 est la moyenne arithmétique des w0 des deux joueurs, ce qui montre que la formule fait une sorte de moyenne pondérée par la logique : un joueur ne progresse dans le classement que s’il bat des plus forts que lui, et ne régresse que s’il perd contre des plus faibles.

Voilà. Le principe est le même pour le calcul de la “bonification de match” R,  mais  la formule est illisible dans le document officiel… Ca a l’air d’être la même que pour W sauf qu’on utilise un coefficient 1/6 au lieu de 1/2. Si j’ai bien compris le reste du règlement, cette “surprime de risque” s’applique dès que le joueur dispute son 6ème tournoi de l’année ou son 5×6 = 30ème match, mais l’Art 5.5 sur les 5 procédures de calcul me semble peu clair…

Note* : Les bases de maths nécessaires pour comprendre la formule sont :

• la connaissance des fonctions exponentielles : e^x signifie le nombre e à la puissance x. Sur une bonne calculatrice, c’est souvent la touche [EXP] qui calcule ceci.
• la fonction ln(x) représente le “logarithme néperien” qui est la fonction inverse de l’exponentielle : ln(e^x) = e^ln(x) = x . Sur les calculatrices c’est [LN], parfois [LOG] mais il faut faire attention à ne pas confondre avec le log base 10 qui donne log(1000)=3
• la somme notée par Σ permet d’additionner un nombre de termes “indicés” comme indiqué sous le Σ: i=1 indique que la variable i vaut 1, puis 2 etc jusqu’à la valeur N indiquée au dessus du Σ.

Posted in Maths, Sport, Suisse  Tagged: classement, tennis